Ｃｈａｐ．３ ＡＮＤ，ＯＲ，ＮＯＴ回路をつくる

この章では、ラダー図シーケンス図でＡＮＤ，ＯＲ，ＮＯＴを作ってみます。

３．１ ＡＮＤ回路
図３．１は、ラダー図シーケンス図で表現したＡＮＤ回路です。
図３．１で、押ボタンスイッチＰＢ１、ＰＢ２の両方を押すと、リレーＲ１のコイルに電流が流れます。
これを式で表すと

Ｒ１ ＝ ＰＢ１ ａｎｄ ＰＢ２

となります。

図３．１ ＡＮＤ回路 （Ｒ１＝ ＰＢ１ ａｎｄ ＰＢ２）

３．２ ＯＲ回路
 図３．２は、ラダー図シーケンス図で表現したＯＲ回路です。
図３．２で、押ボタンスイッチＰＢ１、ＰＢ２のどちらか一方（または両方）を押すと、リレーＲ１のコイルに電流が流れます。
これを式で表すと

Ｒ１ ＝ ＰＢ１ ｏｒ ＰＢ２

となります。

図３．２ ＯＲ回路 （Ｒ１＝ ＰＢ１ ｏｒ ＰＢ２）

３．３ ＮＯＴ回路
 図３．３は、ラダー図シーケンス図で表現したＮＯＴ回路です。
図３．３で、押ボタンスイッチＰＢ１を押すと、リレーＲ１のコイルに電流が流れ、Ｒ１のｂ接点が非導通になるため、リレーＲ２のコイルには電流が流れません。
逆に、押ボタンスイッチＰＢ１を離すと、リレーＲ１のコイルに電流が流れないため、Ｒ１のｂ接点が導通になり、リレーＲ２のコイルに電流が流れます。

これを式で表すと、ＰＢ１とＲ２の関係は

Ｒ２ ＝ ｎｏｔ ＰＢ１

となります。

図３．３ ＮＯＴ回路 （Ｒ２ ＝ ｎｏｔ ＰＢ１）

３．４自己保持回路
 ここまでで、ラダー図シーケンス図でＡＮＤ，ＯＲ，ＮＯＴ回路が作れることがわかりました。
ＡＮＤ、ＯＲ、ＮＯＴ回路さえ作れれば、これらの組み合わせで複雑な論理回路を組み立てることができます。
原理的には、加算器を作って、それを組み合わせてリレー計算機を作る事も可能です。
リレー計算機ではありませんが、ここでラダー＾図シーケンス図で構成した記憶回路を紹介します。
図３．４がその回路で、自己保持回路と呼ばれています。

図３．４ 自己保持回路

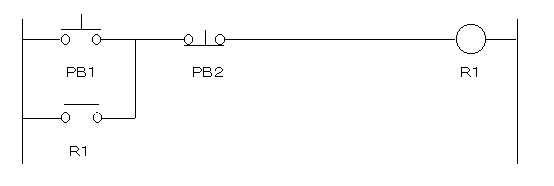この回路の動作は次の通りです。

（１）この回路で、ＰＢ１を押すとリレーＲ１のコイルに電流が流れます。
（２）その後、このＰＢ１を離してもリレーＲ１のコイルに電流が流れ続けます。
（ＰＢ１を離してもリレーＲ１のａ接点を通ってリレーＲ１のコイルに電流を供給し続けるため、このような動作をします。）
（３）この状態は、ＰＢ２を押してリレーＲ１のコイルに流れる電流を切ることで（リレーＲ１のａ接点が非導通になり）解除します。

この（１）〜（３）の動作は、ＰＢ１をセット入力、ＰＢ２をリセット入力とする記憶動作とみなすことができます。
すなわち、直前に押したスイッチがＰＢ１かＰＢ２かをリレーの状態で記憶しています。

自己保持回路はラダー図シーケンス図の基本的な回路です。
リレーが状態を記憶できるということは、リレー回路自身が、内部状態を持つことができることを意味します。
これにより、リレー回路は現在の工程（作業）がどの段階かを記憶し、その工程に応じた次の動作を行なうことが可能となります。
この考え方は、リレー回路がプログラマブルコントローラのラダー図になっても変わっていません。