初めて訪れる方は「ごあいさつ」からご覧ください。
------------------------------------------------------------
目次
------------------------------------------------------------
ごあいさつ
第1回 z=f(x,y)のグラフ/準備編
第2回 z=f(x,y)のグラフ/プログラミング前編
第3回 z=f(x,y)のグラフ/プログラミング後編
第4回 グラフ表示プログラムをワード化する
ごあいさつ(2021/04/18掲載)(*1)
このページは「超小型記号言語」を使った数値計算とゲームについて書いてあります。
非力な整数型プログラミング言語でどこまでできるか、おおよそ40年前のテーマの再挑戦です。
このページは、他のページが忙しくなると放置されるということを繰り返してきました。(他のページも似たようなものだけど)
気長に見守ってやってください。
なお「超小型記号言語」の開発段階の記事は無かったことに(削除)してありますので、悪しからず。
--------------------
(*1)元々タイトルは無かったのですが「こあいさつ」とタイトルを付けました。
掲載日はタイトルを付けた日付にしてあります。
■第1回 z=f(x,y)のグラフ/準備編(2018/12/09掲載,2020/04/12最終変更)
最初のテーマは、z=f(x,y)のグラフです。
このテーマは、パソコン黎明期にグラフィック機能をアピールするにはうってつけでした。
この記事も、当時のパソコン雑誌を参考にしています。(*1)
ただ、超小型記号言語にはグラフィック機能がありません。
そこで、コマンドプロンプト画面に"*"を表示することでグラフィック機能を代用することとします。
幸いなことに、現在のパソコンではコマンドプロンプト上で400×150以上の文字表示が可能で、当時のパソコンのグラフィック機能と比べ遜色ありません。
さて、今回は3次元空間に、水平方向には直交するx軸、y軸、高さ方向にはz軸があるものとします。
この場合、関数z=f(x,y)は、任意のx,yに対してz軸(高さ)方向にf(x,y)だけ上方向にプロットされます。
このプロットされた点の集まりが、関数z=f(x,y)で表された曲面ということになります。
非常に単純な例ですが、f(x,y)=1であれば、高さ1のところにある水平な曲面(平面)を表します。
次に、2次元であるパソコンのディスプレイ上では、縦方向(下向き)にX軸、水平方向(右向き)にY軸があることとします。
このパソコンのディスプレイ(2次元)に立体的なz=f(x,y)の曲面を表示させるには、曲面をある方向から見た場合に限定してディスプレイに表示 するしかありませ ん。
ここで、任意の方向から曲面を見た時のディスプレイ表示を考えると、たぶん行列とか三角関数が登場してきます。
そっち方面(CG)は私の専門外ですし、どうせ超小型記号言語にはそんな関数(行列とか三角関数)はありません。
ということで、見る方向はある特定の斜め方向に限定することとします。
今回の話は、単純化すると3次元空間の任意の点(x,y,z)を、ある関係式で2次元空間(=パソコンのディスプレイ)の点(X,Y)に変換することです。
では、その変換式は次の図1-1ではどういう式になるでしょうか。
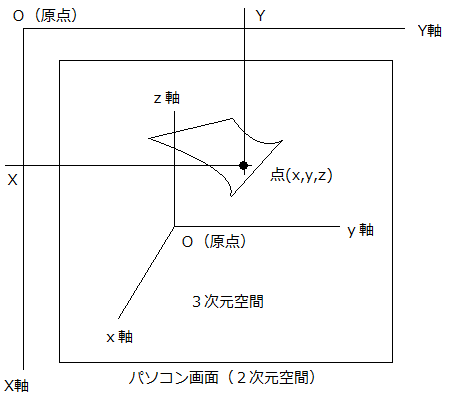
図1-1
まだ、プログラミグしていないので、100%の確証はないのですが、たぶん
X = +x/2 -z
Y = +y -x/2
でしょう。(*2)
図をみれば判ります。(数学は不要です)
それなら、3次元空間の曲面f(x,y)は2次元座標表示では
X = +x/2 -f(x,y)
Y = +y -x/2
となるはずです。(*3)
唐突ですが、今回はここまで。
次回は、実はそう簡単にはいかない諸問題について説明します。
--------------------
「エンサイクロペディア・アスキーVolume3、H68TR 3次元グラフィックス(アスキー出版)」
(*2)(*3)最初はxに係数(1/2)を付けていなかったですが、x軸が真下ではなく斜め左下方向に延びているためx軸の増減は他の軸の半分の効果しか無いと考え、xに係数(1/2)を付けました。
■第2回 z=f(x,y)のグラフ/プログラミング前編(2018/12/24掲載,2019/01/03最終変更)(*2)
前回(第1回)は、関数z=f(x,y)のグラフを表示する仕組みについて説明しました。
理屈としてはこれですべてなのですが、グラフィックライブラリのない超小型記号言語でこれを実現しようとすると、実はそう簡単にはいきません。
今回は、具体的な仕様と設計過程を説明しながら、実はそう簡単にはいかない諸問題の解決方法を示してゆくことにします。
【手順1】画面設計
曲面z=f(x,y)は、縦(x軸)×横(y軸)×高さ(z軸)=100×100×100の立方体の範囲で変化させることにします。
パソコン画面には、この曲面を左斜め上(じゃなくて、右斜め上でした)から見下ろした時の見え方を、縦(S軸)×横(T軸)=50×100の長方形内に表示させます。
なお、前回は画面上の座標を大文字で(X,Y)としていましたが、3次元空間内での座標(x,y,z)と混同しないよう、今回から(S,T)とすることにします。
以上を図2-1に示します。
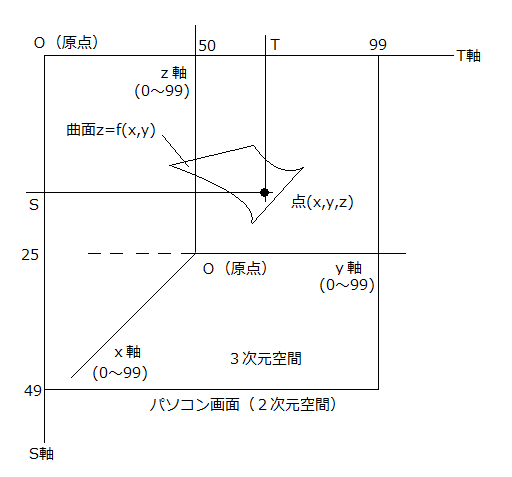
図2-1
【手順2】3D⇒2D変換式
図2-1より、3次元空間内の任意の点(x,y,z)は、パソコン画面上の点(S,T)としては
S = +0.7x -f(x,y)
T = +y -0.7x
となります。
前回は、この式のx係数は0.5だったはずですが、実際に0.5でプログラミングすると理屈通りのグラフとならず、最終的に0.7に変更しました。
0.7の根拠は図2-1でx軸とy軸との関係が直角二等辺三角形の長辺と短辺の関係(1.41:1)にあり、そのおおまかな補正(1.41×0.7=0.987)ということで納得ください。
正直なところ私自身半信半疑で、xの係数が1未満なら0.5でも0.7でも何だって良いような気がするのですが、0.5だとうまくいかないので仕方ありません。
ところで先程の式は原理的な式であって2次元座標と3次元座標の原点位置の差と、各座標の変動範囲を考慮してスケーリングを行うと
S = (+0.7x -f(x,y))/4 +25
T = (+y -0.7x)/2 +50
となります。(*1)
これで、3次元空間内でx,y,f(x,y)がそれぞれ0~99の範囲で変化しても、画面(S=0~49、T=0~99)からはみ出すことは無いはずです。
【手順3】配列の設計とアクセス方法
次に、今回のプログラムで必要な配列を考えます。
まず、画面表示バッファとして要素数50×100=5000個の配列が必要となります。これを
画面表示バッファ Z(0,0)~Z(49,99)
とします。
例えば、配列Z(34,87)に数値42が書き込んである状態で表示ルーチン(まだ説明していないけど)を実行すると、パソコン画面上の座標(34,87)にはASCIIコードで42である"*"が表示されます。
それから、立体を画面表示させる場合「障害物に隠れて見えない面は表示しない」という処理(隠面処理)が必要となります。
次回説明しますが、この隠面処理に横軸(T軸)の各点毎の最大高さと最小高さを記憶する配列を用意します。
最大高さ記憶配列 MAXH(0)~MAXH(99)
最小高さ記憶配列 MINH(0)~MINH(99)
とします。
なお、現状の超小型記号言語(Ver1.4)の配列の要素数は約1000個ですから、これらの配列エリアを準備するのは到底無理です。
ここはあっさり諦めて、超小型記号言語のバージョンアップ(Ver1.4→Ver1.5)で配列エリアを拡張することにしました。
次に、超小型記号言語での配列へのアクセス方法について説明します。 単純な変数Zへのアクセスであれば
#42 Z! (変数Zに数値42を代入)
Z@ ¥ (変数Zの内容を文字表示)
で代入、文字表示できます。
この例では、変数Zの内容は文字コードと解釈され、ディスプレイ上には"*"が表示されます。
1次元配列Z(X)の場合、その実体は「変数Zの番地と変数Xの値を番地と見做して加算した番地」のメモリです。
したがって、配列Z(55)なら変数Zの代わりに「Z #55 +」を使い(逆ポーランド記法ね!)
#42 Z #55 +! (配列Z(55)に数値42を代入)
Z #55 +@ ¥ (配列Z(55)の内容を文字表示)
とします。
超小型記号言語ではアルファベット大文字(A~Z)が単独で現れた場合、数値(0~25)と解釈されることさえ知っていれば問題ないと思います。
では、2次元配列Z(X,Y)はどうするかというと、これを配列Z(X+50*Y)と考えます。(ここではX,Yの範囲が、X=0~49,Y=0~99という前提です)
1次元配列になってしまえば理屈は簡単で、例えば配列Z(13,77)に数値42を代入するには
#42 Z #13 #50 #77 *++! (配列Z(13+50*77)に数値42を代入)
Z #13 #50 #77 *++@ ¥ (配列Z(13+50*77)の内容を文字表示)
とします。
2次元配列Z(13,77)を1次元配列Z(13+50*77)に置き換えているのが判るかと思います。
今回の説明はここまでとします。
次回、後編で表示方法、隠面処理、エッジの強調などの説明をしたいと思います。
理屈はともかく、すでに完成してる3Dグラフィクスプログラム(3dg.vts)を動かしてみましょう。
Windowsパソコン上で動作させるとして、必要なファイルは
超小型記号言語 vts15.zip
サンプルプログラム vts-prg1.zip
です。両方とも「超小型記号言語」のページからダウンロードできます。
2つのファイルを解凍後、同一フォルダに入れ、超小型記号言語の実行ファイルvtsxx15.exeをダブルクリックします。
コマンドプロンプトが立ち上がって"?"を表示したら、"3dg.vts"Enterをキーインすると動作します。
なお、コマンドプロンプトの文字が大きいと正しく曲面が表示されません。
この場合は、1回だけは次の操作を行ってください。 コマンドプロンプトの上側のタイトルバーを右クリックし「プロパティ」を選択
ここで
フォントサイズ=10
フォント=MSゴシック
画面バッファのサイズ=幅120以上、高さ60以上
ウィンドウのサイズ=幅120以上、高さ60以上
であることを確認(必要に応じて変更)
3dg.vts内の関数FNZを書き換えることで、色々な関数の曲面を表示することができます。
サンプルプログラムに曲面定義集が同梱されていますので参考にしてください。(三角関数とかは無理なので悪しからず)
最後に、実行画面を図2-2に示します。(ディスプレイの解像度は1280×1024)
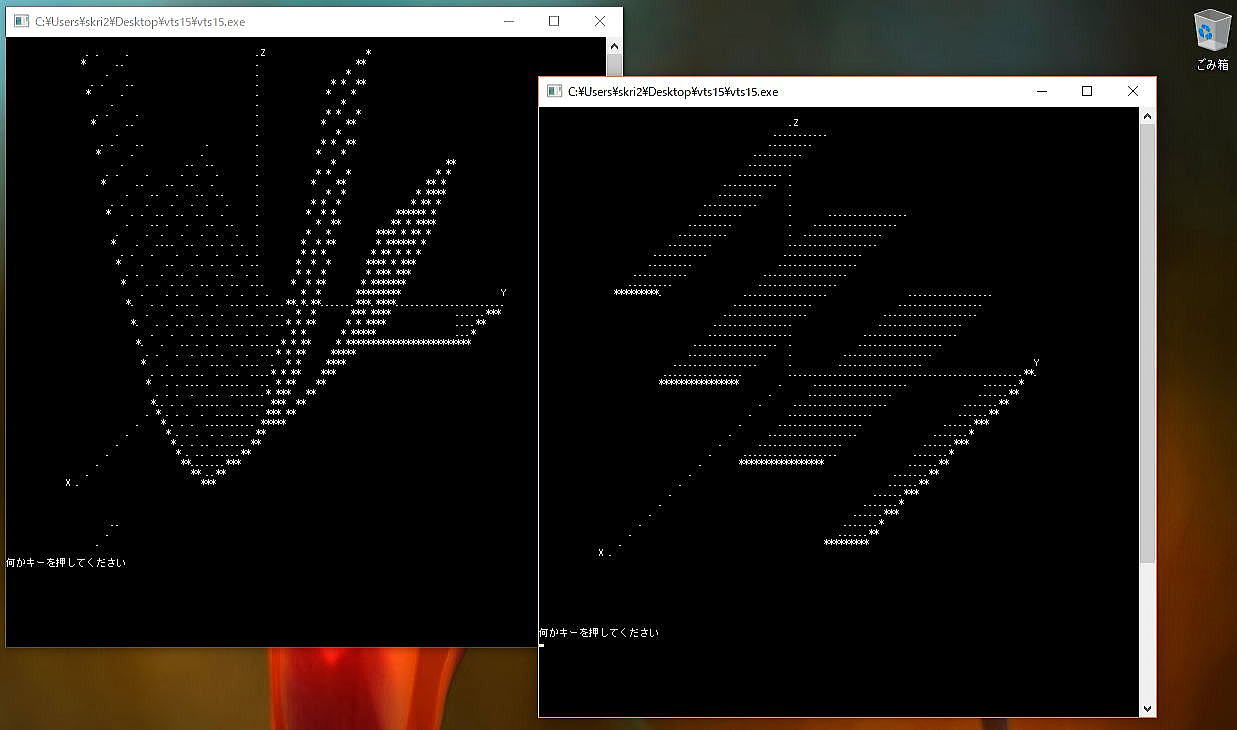
図2-2
では、次回まで。
--------------------
(*1)実際のプログラミングでは、この式を変形して
S = (+7x -10f(x,y))/40 +25
T = (+10y -7x)/20 +50
で計算します。この方が整数演算で誤差が小さくなります。超小型記号言語のコードは逆ポーランド記法なので
X@ #7 * X@ Y@ :FNZ #10 * - #40 / #25 + S!
Y@ #10 * X@ #7 * - #20 / #50 + T!
となります。
(*2)2019/01/02に全面改訂しました。
■第3回 z=f(x,y)のグラフ/プログラミング後編(2019/01/27掲載,2019/02/04最終変更)
前回(第2回)は、具体的な仕様と設計過程(途中まで)を説明しながら、最後に完成したプログラムを実行してみました。
すでにプログラムは完成しているので「実はそう簡単にはいかない諸問題」はすべて解決済みなのですが、一応簡単に概念だけでも解説しておきます。
すでに勝敗が決まった消化試合みたいな気分ですが、頑張りましょう。f(^_^;
【手順4】画面表示と隠面処理(*1)、エッジの強調
まずは画面表示バッファ(配列)に表示データを書き込み、このデータを画面に表示することから始めます。
(1)画面表示
前回、曲面z=f(x,y)とパソコン画面上の点(S,T)の関係は、整数演算で誤差を小さくすることを考慮すると(脚注で)
S = (+7x -10f(x,y))/40 +25
T = (+10y -7x)/20 +50
と説明しました。
そこで、この式に従ってx,yをそれぞれ0から99(*2)まで変化させて、この時の画面表示バッファ(S,T)に"."(ドット)をプロット(文字コードを書込む)ことにします。
画面表示バッファ(S,T)の初期値を" "(空白)の文字コードにしてあるので、全部プロットした時点では、" "または"."のいずれかの文字コードが書き込まれていることになります。
この配列を画面にプリントすれば、" "でも"."でもカーソルは右に進むので画面上に"."がプロットされた曲面が表示されます。
これが画面表示ルーチンで簡単ですが100文字ごとに改行を挟み込みます。この理由は説明不要ですよね。
(2)隠面処理
隠面処理とは、目の前に物体があればその後の物体は隠れて見えないようにする処理です。
現実世界ではこの事実をあたりまえに受け入れていますが、今回の曲面z=f(x,y)も自分で自分の曲面の他の部分を隠す場合があります。
これをきちんと「見えない」ように処理してあげないと立体には見えません。(動いていればまだマシかもしれませんが…)
具体的には(1)で説明した画面表示バッファに書き込むとき
・書き込む順番は、視点から見て手前から奥の順(x=99,98,97,…,2,1,0)とする(*2)
・このとき手前に曲面があれば、隠れて見えないはずなので"."は書き込まない
とします。
手前の曲面とは、現時点までに画面に書き込んだSの最小値~最大値の範囲です。
前回ちょっとだけ触れた
最大高さ記憶配列 MAXH(0)~MAXH(99)
最小高さ記憶配列 MINH(0)~MINH(99)
は、この判定を行うためのもので、もし点(S,T)が
MAXH(T)≦S≦MINH(T)
なら書き込みを行わないようにします。
反対に点(S,T)がこの範囲を外れていれば視点から隠れていないことになるので"."を書き込み、配列MAXH(T)またはMINH(T)更新を更新します。
図3-1は、手前(x=99)から奥(x=0)へ短冊上の面が山形に折れ曲がっている曲面です。
縦位置Tに注目すると、おもて面は通常通り書き込みますが、裏面(図で白丸の部分)は、MAXH(T)≦S≦MINH(T)が成立するため書き込みません。
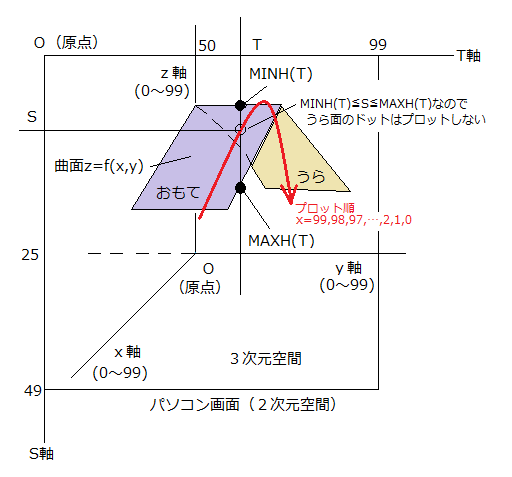
図3-1
(3)エッジの強調
これはおまけみたいな機能ですが、隠面処理でMAXH(T)より大きい、すなわち手前のプロットのときだけ"."ではなく"*"を使用すると、手前の曲面の端が強調され曲面の境界が見やすくなります。
試しに追加した処理ですが、あまりにも見やすいのでそのまま残してあります。
前回の実行画面(図2-2)でその効果が判ると思います。
さて、以上で3回に渡った「z=f(x,y)のグラフ」は今回で終了です。
次回のテーマは決まっていませんが、また近いうちにお会いしましょう。
--------------------
(*1)参考文献
「エンサイクロペディア・アスキーVolume3、H68TR 3次元グラフィックス(アスキー出版)」
「エンサイクロペディア・アスキーVolume3、appleⅡ 3Dグラフィックス(アスキー出版)」
(*2)実際のコードでは、すべてのx,yで計算をするのではなく、xは4つ飛びに、yは2つ飛びで計算しています。
画面の解像度が低い(粗い)のでこれで十分ですし、計算時間も短くなります。
それからxは99ではなく100から始めています。
すなわち、xは100,96,92,…の順に、yは0,2,4,…の順に計算しています。
■第4回 グラフ表示プログラムをワード化する(2025/08/02掲載,2025/08/11最終変更)
第1回~第3回では関数z=f(x,y)のグラフ(曲面)を表示するプログラム3DG.VTSを作成しました。
このプログラムは超小型記号言語を立ち上げ、「?」表示に続いて
?3DG.VTS
と入力することで動作します。
ここでグラフ表示させる関数z=f(x,y)は、プログラム(3DG.VTS)内のワードFNZで定義してあります。
したがって関数を変更したい場合は、このFNZの定義(下線部)を書き換える必要があります。
(7)(*** DEF FUNCTION ***)
{FNZ :SWP :DRP #33 / #33 * #100 :SWP - } (<---KONO TEIGI WO KAKIKAERU!!!)
好みの問題と思うのですが、私としては表示させる関数z=f(x,y)を変更する度に、毎回プログラムをエディタで書き換えるのはちょっと野暮ったい気がしています。
誰がこのプログラムを作ったのかと突っ込まれると、何も言えないのですが… f(^_^;
そこで今回は、プログラムからこの関数定義部分を切り離し、実行時にキーボードから関数(=FNZの定義)を入力できるように改造することにします。
とりあえず改造したものを実行してみましょう。
超小型記号言語を立ち上げ、「?」表示に続いて
?>:3DGZXY {FNZ :SWP :DRP #33 / #33 * #100 :SWP - }
と1行プログラムをキーインすると、階段状のグラフが表示されます。グラフ表示後、今度は「?」表示に続いて
?>:3DGZXY {FNZ :SWP :DRP #50 - :DUP * #30 / #100 :SWP - }
と1行プログラムをキーインすると、今度は凸形の2次曲面のグラフが表示されました。
うまく動いているようです。
ここで、キーインした1行の動作を追ってみます。
まず、最初の「>」は超小型記号言語ver1.8以上(*1)でサポートしているダイレクトモードで、先頭が「>」だとファイル名の代わりに「>」以降の1行をその場で実行します。
したがって、最初に実行するのは「:3DGZXY」ですが、これは「:」がついているので「ワード」です。
ワード「3DGZXY」は、ざっくり言うとプログラム「3DG.VTS」から関数定義部分を除いてワード化したものと思ってください。
このワード「3DGZXY」の定義は、ユーザディクショナリ(usr.dic)に登録してあります。
そして、次に実行するのは{FNZ … }となるはずですが、これは「ワード定義」なので超小型記号言語の文法規則によりここで実行終了となります。
では、このワード「FNZ」はいつ実行されるかというと、実はワード「3DGZXY」内で呼び出されています。試しに
?>:3DGZXY
のみをキー入力すると、FNZの定義がどこにも見つからないので「WORD NOT FOUND =FNZ」というメッセージを連続表示(暴走?)します。(*3)
さて、動作が理解できたところで、実際にプログラム「3DG.VTS」をワード化する改造を見てみましょう。
下のリスト(ピンク色)が元ネタのプログラム3DG.VTSで、これをワード化してユーザディクショナリに登録する改造を青字で追記してあります。
【改造1】プログラム先頭から(6)までを " {3DGZXY" と "}" で囲って、これをユーザディクショナリ(usr.dic)にコピペする
{3DGZXY
"*** 3D GRAPHICS ***";
(1)(*** INIT 2D =50*100 ***)
#0 N!
[a
#32 Z N@ + !
N@ #1 + N!
N@ Z #5000 + < a]
(途中省略)
(6)(*** DISP GRAPH ***)
#12 \
:3DG
}
【改造2】(7)は使用しない (ユーザディクショナリにはコピペしない)
(7)(*** DEF FUNCTION ***)
{FNZ :SWP :DRP #33 / #33 * #100 :SWP - } (<---KONO TEIGI WO KAKIKAERU!!!)
【改造3】(8)からプログラム末尾までを、ユーザディクショナリ(usr.dic)にコピぺする
(8)(*** DEF XYZ ***)
{XYZ
#25 S!
#50 T!
(途中省略)
S@ #1 + S!
S@ #50 < a]
}
以上で、ユーザディクショナリには、3DGZXY、XYZ、3DGの3つのワード定義が登録されたことになります。(*2)
さて、これで今回(第4章)の目的は完了したのですが、3つ補足説明をいたします。
【補足説明1】関数Z=f(x,y)とワードFNZとの関係
関数z=f(x,y)を、どうやってワードに置き換えるかをきちんと説明していませんでので、ここで説明します。
関数z=f(x,y)とワードFNZとの関係は図の通りです。

言葉で表現すると「xの値とyの値をスタックにPUSHされた状態でワードFNZを実行すると、スタックにzの値が残るようにFNZを定義する」ことを行います。
「曲面定義集」の例を幾つか見てみましょう。
(1)高さ100の平面 z=100
これは、x、yの値にかかわらず常にzの値は100です。
スタックに入っている2つの数値x、yは使わないので廃棄(DRP)し、代わり数値100をPUSHしてこれをスタックに残します。したがって
{FNZ :DRP :DRP #100}
となります。
(2)X方向の斜面 z=100-x
これは、xのみを使っていて、yの値にかかわらずzの値は100-xです。
スタックに入っている数値yを使わないので廃棄(DRP)した後(この時点ではスタックにxのみ残って入いる)、100をPUSHして100-xを計算、スタックに残します。
「x-100」ではなく「100-x」を計算するので、途中で100とxの入れ替え(SWP)をおこなっています。したがって
{FNZ :DRP #100 :SWP - }
となります。
(3)2次関数(凸形) z=100-(y-50)*(y-50)/30
2次関数z=-(y*y)の図形がx軸方向に平行移動した形のグラフです。
曲線の見栄えを考慮してY軸方向、Z軸方向ににずらし、Z方向に圧縮しています。
数値xは使わないのでスタックトップに移動(SWP)してから廃棄(DRP)しています。詳しい説明は省略しますが
{FNZ :SWP :DRP #50 - :DUP * #30 / #100 :SWP - }
となります。
【補足説明2】Windows11でコマンドプロンプト画面の文字数を変更する方法
第1章の冒頭で説明してありますが、コマンドプロンプト画面に文字を表示することでグラフィック機能を実現しています。
そのためには、コマンドプロンプト画面の文字数を最低でも「幅120、高さ60」は欲しいところです。
第1章を書いている当時(2019年頃)の動作環境はWindows10で、比較的容易にこのコマンドプロンプト画面の文字数を変更できたのですが、現在の動作環境はWindows11で、コマンドプロンプトの扱いがちょっと複雑になっています。
そこで参考までに、試行錯誤で行った「Windows11でコマンドプロンプト画面の文字数を変更する手順」を以下に示します。
(1)スタートボタンを右クリックして表示されたメニューの中から「ターミナル」を選択します。
(2)ターミナル(コマンドプロンプトかも?)が開いたら、タイトルバーの空いている部分を右クリックして表示されたメニューの中から「設定」を選択します。
(3)「スタートアップ」設定画面(下図)が表示されるので、黄色枠の通り設定し、右下の「保存」をクリックします。
その後、左上の赤枠をクリックして表示されたメニューの中から「プロファイル-コマンドプロンプト」を選択します。

(4)「コマンドプロンプト」設定画面が表示されたら、さらにその中のある「外観」を選択し(下図)、黄色枠の通り設定し、右下の「保存」をクリックします。
右上の☒をクリックし「すべてのタブを閉じますか?」と聞かれたら「すべて閉じる」ボタンを押下します。

これで、次回からは超小型記号言語を立ち上げると「120×60のコマンドプロンプト画面」になっているはずです。(←あまり自信が無いので間違ってたらゴメンです)
【補足説明3】スタック操作ワードの動作(*4)
関数z=f(x,y)のワードFNZには、DUP、SWPなどのスタック操作ワードが使われていています。
これらのワードはシステムディクショナリ(sys.dic)の中で定義してあり、動作はFORTH言語とコンパチなのですがワードの文字数の制約で、例えばFORTH言語の「SWAP」を超小型記号言語では「SWP」と3文字で短縮表記しています。
なお、現在この制約は解消されていて「SWP」と「SWAP」の両方の表記が使えるようになっています。(SWPを使ってSWAPをワード定義しています)
以下は、この超小型記号言語のスタック操作ワードの動作説明です。
| ワード名 (短縮表記) |
動作 |
| DUP | 1番目のスタックのデータのコピーを、スタックにプッシュする |
| DROP (DRP) | 1番目のスタックのデータを、スタックから除去する |
| SWAP (SWP) |
1番目と2番目のスタックのデータを、交換する |
| OVER (OVR) | 2番目のスタックのデータのコピーを、スタックにプッシュする |
| ROT | 3番目のスタックのデータを、1番目のスタックに移動し、元の1番目と2番目のデータは2番目と3番目に移動する ※3個のデータの回転(ROTate) |

今後は、システムディクショナリの充実を考えています。
その時、必要があれば処理系本体の改造も行うつもりです。
--------------------
(*1)ダイレクトモードはVer1.7からサポートしているのですが、ワード「:xxxx」を実行すると画面に「SERCH=xxxx」を出力するという不具合があり、今回のプログラミングには適しません。
(*2)このユーザディクショナリ(usr.dic)は、本ホームページの「超小型記号言語」からダウンロードできます。サンプルプログラムVer2.xに同梱してあります。
(*3)Ver1.9以降では「WORD NOT FOUND =FNZ」というメッセージを表示した後、実行停止します。
(*4)参考文献
「実用FORTHテクニック入門(西川利男著 誠文堂新光社)」
このソフトウェアに関するご意見・ご質問等をお待ちしています。
to@takami.com (アドレスは半角で入力ください)
[トップページに戻る]