目次次へ番外編 Ｃｈａｐ．５ ラダー図で加算器をつくる（２）

Ｃｈａｐ．４では、全加算器の論理式をラダーに変換して、ＬＤ Ｃｖ！で試しに動作させてみるところまでおこないました。
今回は、この全加算器を４個接続して、４ビットの加算をおこなってみます。
もちろん動作確認は、「番外編の命令語インタプリタ」でおこないます。

５．１ Ｉ／Ｏ番号の割付け
全加算器を４個接続して、図５．１のようにＩ／Ｏ番号を割り付けることにします。
（Ｃｈａｐ．４では、表４．３のようにＩ／Ｏ番号を割り付けましたが、わかりやすい割付になっていなかったので、図５．１の割付に変更します。）

図５．１ Ｉ／Ｏ番号の割付（４ビット加算器）

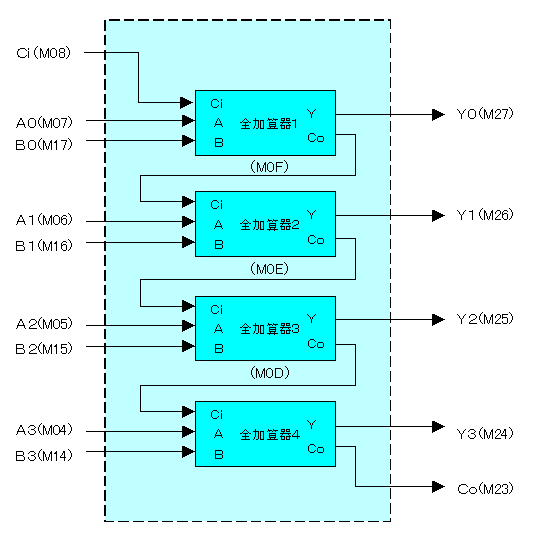図をみると、４個の全加算器のＣｏとＣｉが芋蔓（いもづる）式に配線されています。
この配線は、ラダー図上では接続されているＣｏとＣｉに同一のＩ／Ｏ番号を使うことに相当します。

５．２ 全加算器１の命令語プログラム
では、図５．１の回路のうち１桁分のラダー図を作成し、これを命令語に置き換えてみることにします。
前回おこなったのと同じ方法で、全加算器１をラダー図で表すと、図５．２のようになります。

図５．２ 全加算器１のラダー図

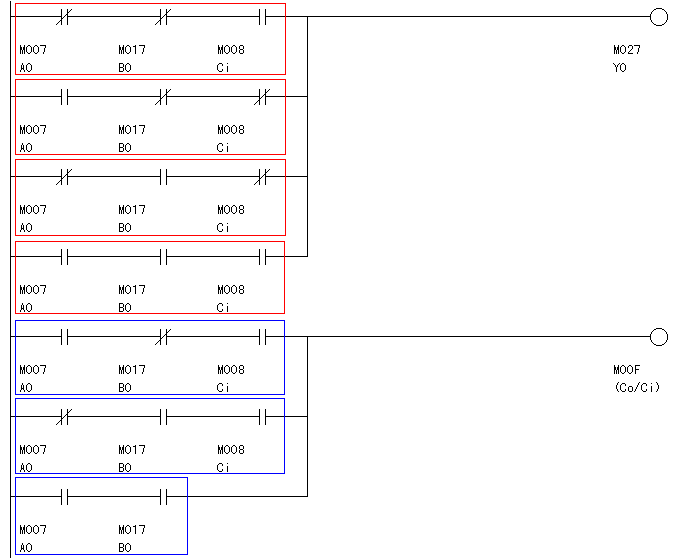このラダー図は赤枠、青枠で囲まれた回路ブロックをそれぞれＯＲ結合しています。
したがって、回路ブロックの結合命令をサポートしていない「番外編の命令語インタプリタ」では、このラダー図を実行することができません。
そこで、これらの回路ブロックを、図５．３のようにいったんコイルＭ４０〜Ｍ４６に置き換えることにします。

図５．３ 図５．２の回路ブロックをコイルに置き換え

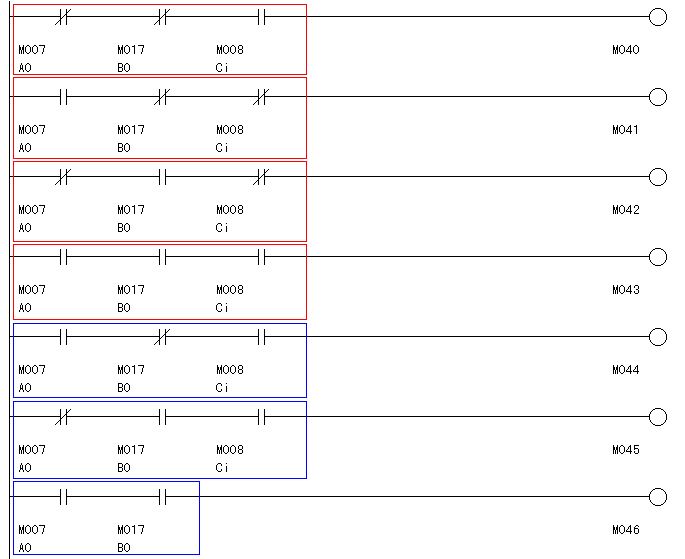回路ブロックをコイルに置き換えたので、今度は図５．４のように「番外編の命令語インタプリタ」でもＯＲ結合が可能です。

図５．４ 全加算器１のラダー図（図５．３の結果を使用）

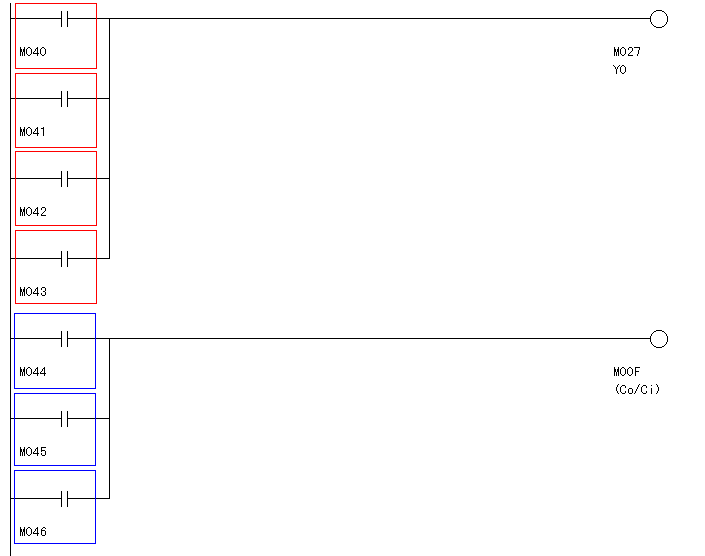図５．３と図５．４を一緒にすると、図５．２のラダー図と等価になります。
図５．３と図５．４のラダー図ならば、「番外編の命令語インタプリタ」でも実行可能な命令語プログラムに変換できます。
手作業で、図５．３と図５．４のラダー図を命令語に変換したのがリスト５．１です。

リスト１ 全加算器５．１の命令語プログラム
/* 全加算器１(1/7) */
LDNOT
7
ANDNOT
17
AND
8
OUT
40
/* 全加算器１(2/7) */
LD
7
ANDNOT
17
ANDNOT
8
OUT
41
/* 全加算器１(3/7) */
LDNOT
7
AND
17
ANDNOT
8
OUT
42		 /* 全加算器１(4/7) */
LD
7
AND
17
AND
8
OUT
43
/* 全加算器１(5/7) */
LD
7
ANDNOT
17
AND
8
OUT
44
/* 全加算器１(6/7) */
LDNOT
7
AND
17
AND
8
OUT
45		 /* 全加算器１(7/7) */
LD
7
AND
17
OUT
46
/* 全加算器１(出力Ｙ０) */
LD
40
OR
41
OR
42
OR
43
OUT
27
/* 全加算器１(桁上げ) */
LD
44
OR
45
OR
46
OUT
F

５．３ ４ビット加算器の命令語プログラム
ここまでで、全加算器１の命令語プログラムができあがりました。
同様にして、全加算器２〜全加算器４の命令語を作成し、全加算器１〜全加算器４を１つのプログラムにして、末尾にＥＮＤ命令を追加したのがリスト５．２です。
（コイルへの置き換えは、４８〜４Ｅ、５０〜５７、５８〜５Ｅを使用しました。）

リスト５．２ ４ビットの加算器の命令語プログラム
/* 全加算器１(1/7) */
LDNOT
7
ANDNOT
17
AND
8
OUT
40
/* 全加算器１(2/7) */
LD
7
ANDNOT
17
ANDNOT
8
OUT
41
/* 全加算器１(3/7) */
LDNOT
7
AND
17
ANDNOT
8
OUT
42
/* 全加算器１(4/7) */
LD
7
AND
17
AND
8
OUT
43
/* 全加算器１(5/7) */
LD
7
ANDNOT
17
AND
8
OUT
44
/* 全加算器１(6/7) */
LDNOT
7
AND
17
AND
8
OUT
45
/* 全加算器１(7/7) */
LD
7
AND
17
OUT
46
/* 全加算器１(出力Ｙ０) */
LD
40
OR
41
OR
42
OR
43
OUT
27
/* 全加算器１(桁上げ) */
LD
44
OR
45
OR
46
OUT
F		 /* 全加算器２(1/7) */
LDNOT
6
ANDNOT
16
AND
F
OUT
48
/* 全加算器２(2/7) */
LD
6
ANDNOT
16
ANDNOT
F
OUT
49
/* 全加算器２(3/7) */
LDNOT
6
AND
16
ANDNOT
F
OUT
4A
/* 全加算器２(4/7) */
LD
6
AND
16
AND
F
OUT
4B
/* 全加算器２(5/7) */
LD
6
ANDNOT
16
AND
F
OUT
4C
/* 全加算器２(6/7) */
LDNOT
6
AND
16
AND
F
OUT
4D
/* 全加算器２(7/7) */
LD
6
AND
16
OUT
4E
/* 全加算器２(出力Ｙ１) */
LD
48
OR
49
OR
4A
OR
4B
OUT
26
/* 全加算器２(桁上げ) */
LD
4C
OR
4D
OR
4E
OUT
E		 /* 全加算器３(1/7) */
LDNOT
5
ANDNOT
15
AND
E
OUT
50
/* 全加算器３(2/7) */
LD
5
ANDNOT
15
ANDNOT
E
OUT
51
/* 全加算器３(3/7) */
LDNOT
5
AND
15
ANDNOT
E
OUT
52
/* 全加算器３(4/7) */
LD
5
AND
15
AND
E
OUT
53
/* 全加算器３(5/7) */
LD
5
ANDNOT
15
AND
E
OUT
54
/* 全加算器３(6/7) */
LDNOT
5
AND
15
AND
E
OUT
55
/* 全加算器３(7/7) */
LD
5
AND
15
OUT
56
/* 全加算器３(出力Ｙ２) */
LD
50
OR
51
OR
52
OR
53
OUT
25
/* 全加算器３(桁上げ) */
LD
54
OR
55
OR
56
OUT
D		 /* 全加算器４(1/7) */
LDNOT
4
ANDNOT
14
AND
D
OUT
58
/* 全加算器４(2/7) */
LD
4
ANDNOT
14
ANDNOT
D
OUT
59
/* 全加算器４(3/7) */
LDNOT
4
AND
14
ANDNOT
D
OUT
5A
/* 全加算器４(4/7) */
LD
4
AND
14
AND
D
OUT
5B
/* 全加算器４(5/7) */
LD
4
ANDNOT
14
AND
D
OUT
5C
/* 全加算器４(6/7) */
LDNOT
4
AND
14
AND
D
OUT
5D
/* 全加算器４(7/7) */
LD
4
AND
14
OUT
5E
/* 全加算器４(出力Ｙ３) */
LD
58
OR
59
OR
5A
OR
5B
OUT
24
/* 全加算器４(桁上げ) */
LD
5C
OR
5D
OR
5E
OUT
23
END

このリスト２は、番外編の命令語インタプリタで実行することが可能です。

５．４ ４ビット加算器の実行
では、リスト２の命令語プログラムを実際に動かしてみることにしましょう。
例として、７＋１０＝１７（２進数で、０１１１＋１０１０＝１０００１）を計算させてみます。
操作手順は、（１）〜（５）のとおりです。

（１）リスト２のプログラムをテキストエディタで作成し、適当なファイル名で保存します。
（２）番外編の命令語インタプリタを起動します。
（３）「ファイル読み込み」ボタンをクリックし、（１）で作成したファイル名を指定し、プログラムを読み込みます。
（４）「データ入力」ボタンをクリックし、図５．５のように数値を１ビットずつ入力します。

図５．５ データ入力の書式

ここでは数値１０と数値７なので、表５．１のように各ビットを入力します。

表５．１ 各ビットの入力値
数値 入力操作
数値７
（２進数で０１１１）		 ・アドレス０４に、０を入力
・アドレス０５に、１を入力
・アドレス０６に、１を入力
・アドレス０７に、１を入力
数値１０
（２進数で１０１０）		 ・アドレス１４に、１を入力
・アドレス１５に、０を入力
・アドレス１６に、１を入力
・アドレス１７に、０を入力

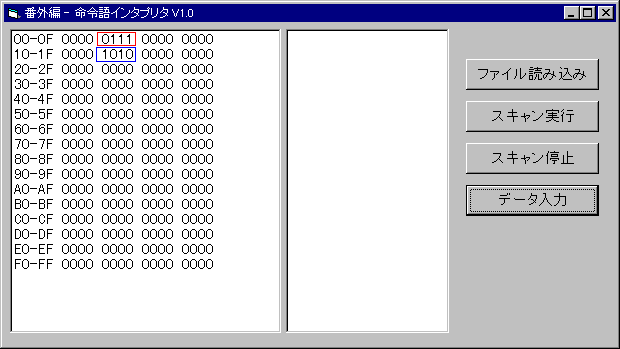
数値をすべて入力すると、図５．６のようになります。

図５．６ 加算器に７と１０を入力した直後（赤枠が７、青枠が１０）

（５）「スキャン実行」ボタンをクリックし、計算結果を見ます。（図５．７）

図５．７ 加算器で７＋１０を実行したところ
（ピンク枠が計算結果の１１Ｈ、すなわち１７）

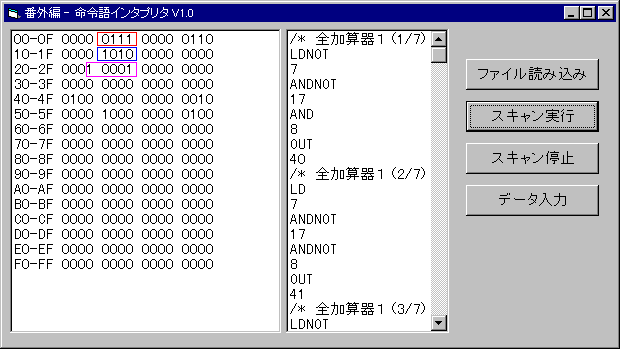計算結果は、２４〜２７に出力され、計算の結果桁上げは、２３に出力されます。
図５．７では、０１１１＋１０１０＝１０００１を計算していることがわかります。

数値を変えてみて、正しく加算していることを確かめてみてください。
たとえば、次のような計算です。

（１）４＋８＝１２ （０１００＋１０００＝０１１００）
（２）１３＋１５＝２８（１１０１＋１１１１＝１１１００） （注）２８は１６進数で１Ｃ、２進数で１１１００

５．５ 実際のリレー回路へ適用する場合
これまでで、ラダー図をコンピュータ上でシミュレーションして、４ビットの加算がおこなえたことを確認できました。
シミュレーションできたのですから、実際にリレーを組み合わせても、加算器ができるはずです。
ただし、実際にリレーでラダー図の配線をおこなう場合は、そのリレー（部品）に内蔵している接点の数に制限があるため、使用する接点の数を満たすだけのリレーが必要となります。

さて、次回はメモリに挑戦します。
ここから先は、あまり考えていないので、色々な問題が出てくるかもしれません。

目次次へ