初めて訪れる方は「ごあいさつ」からご覧ください。
------------------------------------------------------------
目次
------------------------------------------------------------
ごあいさつ
第1回 ルート2の計算
第2回 πの計算/改定版
第3回 ライフゲーム/準備編
第4回 ライフゲーム/本編
第5回 ライフゲーム/動作編
第6回 山崩しゲーム/準備編
第7回 山崩しゲーム/続準備編
第8回 山崩しゲーム/本編
第9回 山崩しゲーム/解説編
第10回 Brainfuck/準備編
第11回 Brainfuck/サブルーチン編
第12回 Brainfuck/本編
第13回 Brainfuck/改造編
第14回 Brainfuck/実行編
第15回 素数の計算
第16回 自然対数の底eの計算
第17回 スライドパズル
------------------------------------------------------------
記事中のプログラム・資料
------------------------------------------------------------
※本記事中で使用するプログラム・資料は下のリンクからダウンロードできます
プログラム1(ルート2の計算),2(πの計算),4(ライフゲーム) (list_su1.txt)
プログラム8(山崩しゲーム) (list_su2.txt)
プログラム11(Brainfuck) (list_su3.txt)
プログラム13(Brainfuck) (list_su3a.txt)
プログラム15(素数の計算),16(自然対数の底eの計算) (list_su4.txt)
プログラム17(スライドパズル) (list_su5.txt)
ターミナルソフト(ZTERM!)を使用すると、マイクロBAICのプログラムをPC~マイコンボード間で転送できます。
ZTERM!上で~(チルダ)キーを押下することで、この機能が動作します。
■ごあいさつ(2016/09/11掲載,2021/11/28最終変更)
ここでは、マイコンキットZCPU1シリーズ、またはその互換ボード(*1)のマイクロBASICを(*2)使って、数値計算とゲームプログラミングに挑戦します。
この言語のプログラムの見た目は一般のBASICとかなり違うのですが、次の対応ルールで簡単に置き換え可能です。(*4)
マイクロBASICの実行環境が無い方は、BASICに置き換て実行してみてください。
マイクロBASIC 一般のBASIC
--------------------------------------------------------
#=行番号 GOTO 行番号、またはGOSUB 行番号
#=! RETURN
#=条件式*行番号 IF 条件式 THEN (GOTO) 行番号
?=変数名 PRINT 変数名
変数名=? INPUT 変数名
゛文字列゛ PRINT ゛文字列゛
(コメント文字列 REM コメント文字列
@(引数) 配列変数名(引数)
#=1 RUN
0 LIST
&=264 NEW
なお、今回使用するマイクロBASICは小さな処理系なので制限事項が色々あります。特に
・サブルーチンの入れ子が不可能、かつサブルーチン中での#=行番号に使用制限がある(*3)
・数式の括弧と配列の括弧が兼用で、合わせて1レベルのみ
・演算子(+-*/)の優先順位が無い
ことにご注意ください。
ここで紹介するプログラムのリストは、ページ先頭にある「記事中のプログラム・資料」からダウンロードできます。
専用のターミナルソフト(ZTERM!)を使用した場合、ダウンロードしたプログラム(テキストファイル)をマイクロBASICにロードすることができます。
--------------------
(*1)互換ボードは市販部品を集めて製作可能です。詳しくは「eZ8マイコンボードの自作」をご覧ください。
(*2)一般に、整数しか扱えない処理系のサイズが2Kバイト程度のBASICをタイ二―BASICと呼んでいます。
マイクロBASICはこれより小さな処理系で、VTL(Very Tiny Language)が歴史的に有名です。
今回使用するマイクロBASICの表記はVTLと類似していますが、コンパチ(完全互換)ではありません。
(*3)第9回で、制限の回避方法について説明しています。
(*4)Brainfuckに関しては、ハードウェアに依存した機能を使っているので単純な置き換えではできません。というか、文字列変数を使えばもっと簡単にプログラムできます。
■第1回 ルート2の計算(2016/09/11掲載,2021/04/18最終変更)
最初のテーマはルート2の計算です。
ZCPU1シリーズのマイクロBASIC(以後、単にマイクロBASICと呼びます)が扱える数は0~65535の整数です。
2の平方根の計算とは、□×□=2となる□を求めることですが、整数しか扱えないマイクロBASICでは一工夫必要です。
ここでは、□×□=20000となる□を求め、最後に求めた数値□を2桁ずらして読むこととします。
具体的には□×□を1から順に計算し、計算結果が20000を超えた時点の□を2の平方根としています。
なお、行番号1070の#=50000は、他のプログラム(第2回以降)と共存させるための工夫で数値計算とは関係ありません。
【プログラム1】ルート2の計算(#=1000で実行)
1000 (PROGRAM1)
1005 "ROOT 2"
1010 A=1
1020 #=(A*A>20000)*1050
1030 A=A+1
1040 #=1020
1050 ?=A;
1060 " ";
1070 #=50000
実行結果は、142となります。
2桁ずらして読むと1.42となり、真値1.4142…に対し一応2桁まで一致しました。
なお、行番号1020で、20000を30000および50000に書き換えると、それぞれルート3、ルート5の計算をします。
それにしても有効桁数が少なすぎます。
原因は、計算過程に2乗の計算(□×□)があり、計算結果が大きくなってオーバーフローするのを回避しなければならないためです。
次回は、2乗の計算を含まない円周率の計算を予定しています。(今度はもう少し有効桁数が増やせそうです)
■第2回 πの計算/改定版(2016/09/22掲載,2016/10/23最終変更)(*1)
π(円周率)の計算は、次のライプニツの式(*2)で求めることができます。
π/4=1-(1/3)+(1/5)-(1/7)+(1/9)-(1/11)…
この計算式はオーバーフローの原因となる掛け算を使用しないため、マイクロBASICには最適です。
とりあえず、両辺を4倍してπの式にします。
π=4-(4/3)+(4/5)-(4/7)+(4/9)-(4/11)…
さらに、両辺に10000を掛けます。
10000π=(40000/1)-(40000/3)+(40000/5)-(40000/7)+(40000/9)-(40000/11)… (式1)
この式の右辺を見ると、計算途中で40000を超えることは無く、オーバーフロー(65535を超える)は起こりません。
しかも、計算結果がπの10000倍なので、小数点を4桁ずらせばそのままπの値になりそうです。
【プログラム2】πの計算(ライプニツの式)(#=2000で実行)
2000 (PROGRAM2)
2010 "PAI"
2020 A=1
2030 P=0
2040 P=P+(40000/A)
2050 ?=P
2060 A=A+2
2070 P=P-(40000/A)
2080 A=A+2
2090 ?=P;
2100 " : ";
2110 ?=A
2120 #=2040
このプログラムは永遠にループします。
計算結果の最初の数値はπの計算値、2番目の数値は(式1)の級数の分母1,3,5,7…の値です。
(式1)で約5000個の和まで加算したところでESCキーで停止させました。
結果は、(小数点を4桁ずらして読んで)3.1406と3.1409の間で振動しています。
真値3.141592…に対し一応3桁まで一致しました。
--------------------
(*1)計算経過がわかるようにプログラムを書き換え、改訂版として再掲載しています。
(*2)参考文献「世界大百科事典4(平凡社)」円周率
■第3回 ライフゲーム/準備編(2016/10/09掲載,2021/04/18最終変更)
ゲームと呼んでいますが、内容は単純化された生態系のシミュレーションです。
有名なゲームなのでご存知の方も多いと思います。(*1)
配列と整数演算が使えるコンピュータであればプログラムできるため、マイクロBASICにはうってつけです。
なお、今回のテーマはマイコンキットの16文字×2行の液晶ディスプレイでは表示に限界があり断念しました。
多くの行を表示するため、マイコンキットにUSB-シリアルケーブルを介して入出力装置(ターミナル)を接続します。(互換ボードでもOKです)
ターミナルは、具体的にはターミナルソフトを動作させたパソコンです。
これから数回に渡ってプログラミングしてゆきます。
今回は準備編ということで仕様決めを行います。
まず、ルールの説明です。
10×10のマス目(*2)の大きな盤(将棋盤みたいなもの)に、初期値として適当な場所に数個の石(碁石みたいなもの)を置きます。
石は1つの生物(個体)で、次のルールに従って石の周囲の環境が良いと生存または発生し、悪いと死滅します。
ルール1-過疎状態(周囲の8個のマス目の石が0~1個)であれば、1世代後は死滅(石を取り除く)
ルール2-適正状態(周囲の8個のマス目の石が2~3個)であれば、1世代後は生存(石をそのままにしておく)
ルール3-過密状態(周囲の8個のマス目の石が4~8個)であれば、1世代後は死滅(石を取り除く)
ルール4-石が無い箇所の周囲8個のマス目の石が3個であれば、1世代後は発生(盤に石を置く)
なお、10×10のマス目のうち、周囲4辺(境界)のマス目は上下左右のいずれかが存在しません。
ここでは次のように境界を処理することにします。
境界処理-周囲4辺のマス目は初期状態のままで石が変化しないもの(固定)とする。(*4)
10×10のマス目の場合は、世代更新処理を行う計算対象は中央の8×8のマス目(下図の□の部分)のみです。
ただし、個々の石について「周囲の8個のマス目の石の数を計算」するときには、境界の石(■)の状態も計算に含めます。
0123456789
0■■■■■■■■■■
1■□□□□□□□□■
2■□□□□□□□□■
3■□□□□□□□□■
4■□□□□□□□□■
5■□□□□□□□□■
6■□□□□□□□□■
7■□□□□□□□□■
8■□□□□□□□□■
9■■■■■■■■■■
一次元配列しか持たないマイクロBASICでは、マス目は@(0)~@(99)で表現します。
したがって世代更新処理は、石のマス目を@(n)とした場合
@(n-11),@(n-10),@(n-9),@(n-1),@(n+1),@(n+9),@(n+10),@(n+11)
の和に対しルール1~ルール4を適用することになります。
今回はここまでとします。
ここまでのところ、アルゴリズムに特に問題はありません。
メモリ容量に少し不安があるところですが、こればかりは作ってみないと判りません。(*3)
--------------------
(*1)マーティン・ガードナーがScientific American誌のコラムで紹介(作者は別)したゲームです。
(*2) 最初16×16のマス目で動作させたのですが、処理時間がかかりすぎたため10×10に変更しました。
(*3)参考文献
「Make:Vol.04(オライリー・ジャパン)」数術師
「エンサイクロペディア・アスキーVolume3(アスキー出版)LIFE GAME
(*4)境界処理の説明を解り易く書き直しました。
■第4回 ライフゲーム/本編(2016/10/23掲載)
前回はライフゲームのルール説明と、境界部分の扱いについて説明しました。
今回はプログラムを作成し動作させてみます。
まず、変数を割り当ててゆきます。
配列 @( 0)~@( 99) 個体分布マップ(10×10のマス目、個体存在しない=0、個体存在する=1)
配列 @(100)~@(199) 周囲個体合計表(10×10のマス目、0~8の値をとる)
変数 X X座標(0~9)
変数 Y Y座標(0~9)
変数 G 世代数(1,2,3,…)
変数 S 作業変数(周囲個体合計)
変数 N 作業変数(1次元座標=Y*10+X)
変数 A,B 作業変数
ゲームのアルゴリズムは次の通りとします。
ステップ1 個体分布マップを初期化(ゼロクリア)する
ステップ2 個体分布の初期値(XY座標)を聞き、個体分布マップに1を書込む(範囲外の座標入力でステップ3へ)
ステップ3 個体分布マップを画面表示
ステップ4 個体分布マップを元に周囲個体数を計算、周囲個体合計表に書込む
ステップ5 個体分布マップと周囲個体合計表にルールを適用し、個体分布マップを更新後、ステップ3に戻る
以上で設計終了です。
では、この設計通りプログラミングしていきます。
【プログラム4】ライフゲーム(#=3000で実行)
3000 (PROGRAM4)
3010 "LIFE GAME"
3020 (STEP1)
3030 N=0
3040 @(N)=0
3050 N=N+1
3060 #=(N<100)*3040
3100 (STEP2)
3110 "X=";
3120 X=?
3130 #=(X>9)*3200
3140 "Y=";
3150 Y=?
3160 #=(Y>9)*3200
3170 @(Y*10+X)=1
3180 #=3110
3200 (STEP3)
3210 G=0
3220 G=G+1
3230 "GEN=";
3240 ?=G
3250 Y=0
3260 X=0
3270 #=@(Y*10+X)=1*3300
3280 ".";
3290 #=3310
3300 "*";
3310 X=X+1
3320 #=(X<10)*3270
3330 Y=Y+1
3340 ""
3350 #=(Y<10)*3260
3360 ""
3400 (STEP4)
3410 Y=1
3420 X=1
3430 N=Y*10+X
3440 S=@(N-11)+@(N-10)+@(N-9)
3450 S=S+@(N-1)+@(N+1)+@(N+9)
3460 S=S+@(N+10)+@(N+11)
3470 @(N+100)=S
3480 X=X+1
3490 #=(X<9)*3430
3500 Y=Y+1
3510 #=(Y<9)*3420
3600 (STEP5)
3610 Y=1
3620 X=1
3630 N=Y*10+X
3640 A=@(N)
3650 B=@(N+100)
3660 #=(A=1)*(B=2)*3700
3670 #=(B=3)*3700
3680 @(N)=0
3690 #=3710
3700 @(N)=1
3710 X=X+1
3720 #=(X<9)*3630
3730 Y=Y+1
3740 #=(Y<9)*3620
3750 #=3220
ルールの適用部分は行番号の3660~3700です。
次回は、動作検証を兼ねていくつかのパターンを動作させみます。
■第5回 ライフゲーム/動作編(2016/10/30掲載,2021/04/19最終変更)
前回でプログラミングは終了したので、動作検証してみまます。(説明の都合、個体をA、B、C…とします)
(1)個体が1個(結果:死滅する)
Aの周囲には個体がないため、2世代目(GEN=2)で死滅しました。
0123456789
0・・・・・・・・・・
1・・・・・・・・・・
2・・・・・・・・・・
3・・・A・・・・・・
4・・・・・・・・・・
5・・・・・・・・・・
6・・・・・・・・・・
7・・・・・・・・・・
8・・・・・・・・・・
9・・・・・・・・・・
(2)個体が2×2個(結果:変化せず)
各個体の周囲には3個の個体がある(Aの周囲ならBCDの個体、Bの周囲ならACDの個体、…)ので生存しますが、発生(増殖)しません。
すなわち、個体の分布パターンは変化しません。
0123456789
0・・・・・・・・・・
1・・・・・・・・・・
2・・・・・・・・・・
3・・・AB・・・・・
4・・・CD・・・・・
5・・・・・・・・・・
6・・・・・・・・・・
7・・・・・・・・・・
8・・・・・・・・・・
9・・・・・・・・・・
(3)個体が3×3個(結果:発生(増殖)する)
4隅のACGI以外は過密状態で死滅しますが、個体が無い座標(4,2)などの周囲の個体が3個の箇所があるで発生します。
世代が進むにつれて外に向かって発生(増殖)します。
0123456789
0・・・・・・・・・・
1・・・・・・・・・・
2・・・・・・・・・・
3・・・ABC・・・・
4・・・DEF・・・・
5・・・GHI・・・・
6・・・・・・・・・・
7・・・・・・・・・・
8・・・・・・・・・・
9・・・・・・・・・・
5世代目(GEN=5)のパターンは次の通りになりました。
個体数は初期値の9個(A~I)から20個(A~U)に増えています。
0123456789
0・・・・・・・・・・
1・・・・A・・・・・
2・・・BCD・・・・
3・・E・F・G・・・
4・HIJ・KLM・・
5・・O・P・Q・・・
6・・・RST・・・・
7・・・・U・・・・・
8・・・・・・・・・・
9・・・・・・・・・・
一応うまく動作しているようです。
今回で、ライフゲームは終了とし、次回からはマイコンキットの16文字×2行の液晶ディスプレイで動作できるテーマにする予定です。
では、また。
■第6回 山崩しゲーム/準備編(2016/12/11掲載,2017/01/04最終変更)
※この回(第6回)の説明に誤りがあることに後で気が付いたのですが、そのままにしてあります。訂正は次回(第7回)でおこないます。
石が積まれた山から、2人がルールに従って交互に石を取ってゆき、最後に石を取った方が勝ち(または負け)というゲームがあります。
一番有名なのは3つの山から石を取る「三山崩し」です。
三山崩しは排他論理和を使って最善手が計算できるので、マイコンとの対戦ゲームとしては最適です(*1)。
ここでは、3つの山ではなく、1つの山から石を取ってゆき「最後の石を取った方勝ち」というゲームです。
ただし、好きなだけ石を取って良ければ先手が最初にすべての石を取って先手必勝となってしまい、これではゲームになりません。
参考文献(*2)によれば、このゲームのルールは次の通りです。
ルール1-先手の第1手目では、全部の石を取ってはいけない。
ルール2-以降は、相手が直前に取った石の2倍までの石を取って良い。(たとえば、相手が3個取ったら自分は1~6個の範囲で好きな個数を取れる)
同じく、参考文献(*2)によれば、次の先手必勝法が存在します。
先手必勝法-現在の石の数をフィボナッチ数(*3)の和で表し、その中の一番小さなフィボナッチ数の石を取る
例えば石の数が20個の場合、3つのフィボナッチ数(13+5+2)の和で表せるので、その中の一番小さな数である2個取れば良いことになりま す。
実例として、石の山が15個でコンピュータが先手の場合のゲームの進行を見てみましょう。
・石の数15個(8+5+2)から、コンピュータが2個取る
・残った石の数13個から、人間はルール2により1~4個の範囲で取れるので、ここでは適当に4個取る
・残った石の数9個(5+3+1)から、コンピュータが1個取る
・残った石の数8個から、人間はルール2により1~2個の範囲で取れるので、ここでは適当に2個取る
・残った石の数6個(3+2+1)から、コンピュータが1個取る
・残った石の数5個から、人間はルール2により1~2個の範囲で取れるので、ここでは1個取る(ここらへんで、人間は負けそうなことに気が付き焦 り始めます)
・残った石の数4個(3+1)から、コンピュータが1個取る
・残った石の数3個から、人間はルール2により1~2個の範囲で取れるので、ここでは1個取る(すでに、人間は負けに気が付いています)
・残った石の数2個(2)から、コンピュータが2個取る、最後の石を取った方勝ちなのでコンピュータの勝ち
確かに、この例では先手のコンピュータは、石の数をフィボナッチ数の和で表した時の一番小さな数の石を取ることで勝ちました。
なお、ゲームとして飽きが来ないように毎回変化を持たせ、時には人間が勝つこともあるようにするため、次のように設計することとします。
設計1-最初の石の数は乱数で21~99の範囲とする。
設計2-人間に先手を持たせる
設計3-石の数が21以上のときは、コンピュータは乱数で取る石の数を決める
設計4-石の数が20以下になったら、コンピュータは必勝法(一番小さなフィボナッチ数を取る)に従い石を取る
次回は、この設計でプログラミングを行います。
このゲームは表示が少なくて済むので、マイコンキットZCPU1/K(液表示器2桁)を電池駆動で持ち歩いて遊べそうな気がします。
--------------------
(*1)排他論理和なので、理論上ロジックICでも計算できます。数十年前マイコン雑誌で読んだことがありますが詳しい内容は忘れました。
こういうときは伝家の宝刀、国立国会図書館の出番です。国立国会図書館の説明はコラム「色々」の「いざ、国立国会図書館へ!」を見てね。
(*2)参考文献(翻訳本)「不思議な数列フィボナッチの秘密(日経BP社)」
この本はフィボナッチ数列が、自然界や芸術など意外なところで現れることを紹介していて、山崩しゲーム必勝法はそのうちの1つです。
(*3)フィボナッチ数列{Fn}は、F1=F2=1,Fn=Fn-2+Fn-1で表せる数列 1,1,2,3,5,8,13,21,34,55,89,144,…で、フィボナッチ数はこの各項を意味します。
■第7回 山崩しゲーム/続準備編(2016/12/25掲載,2021/04/19最終変更)
前回(第6回)の冒頭で説明した通り、前回の説明には私のミスで間違いがあります。
間違いは「先手必勝法」の説明です。
(誤)先手必勝法-現在の石の数を「フィボナッチ数の和」で表し、その中の一番小さなフィボナッチ数の石を取る
(正)先手必勝法-現在の石の数を「隣合わないフィボナッチ数の和」で表し、その中の一番小さなフィボナッチ数の石を取る
すなわち、現在の石の数は「フィボナッチ数の和」ではなく「隣合わないフィボナッチ数の和」で表すのが正解です。
そうしないと、その中の一番小さなフィボナッチ数の石を取っても、次に相手(後手)に残りすべてを取られてしまうことがあるためです。
では、実例を考えてみます。
(例1)石の数が5個でゲームが始まった場合
ここで先手が誤って、石の数を普通にフィボナッチ数の和(5=0+2+3)(*1)で表したとします。(隣り合った部分2+3があります)
先手は、必勝法に従ってその一番小さなフィボナッチ(2)個の石を取ります。
後手は、先手が2個取ったので最大4個までの石を取ることができるので、残りの石(3個)を全て取ることができ、後手の勝ちとなります。
先手が負けた原因は「隣合わないフィボナッチ数の和」でなかったからです。
(例2)石の数が17個でゲームが始まった場合
まず、石の数17をフィボナッチ数(1,2,3,5,8,13,21,34,55,89,144,…)の和で表してみます。
次の2つのパターンが考えられます。
パターン1 17=1+0+3+0+0+13 (隣合わないフィボナッチ数の和)
パターン2 17=1+0+3+5+8 (8+5+3の部分で隣り合っているフィボナッチ数の和)
この場合、17をパターン1で表し、その中の一番小さなフィボナッチ数(1)の数の石を取るのが正解です。
これは「相手が直前に取った石の2倍を超える石を取ってはいけない」というルールがあるために、後手は次に残りすべての石を取ることができないた めです。
一般的に石の数がn=0+…+A+0+Bで、ここから先手がA個を取った場合、後手は残りのB個すべてを取ることはできません。
なぜなら、フィボナッチ数の性質からB>2Aであるため、仮に2倍(2A個)取ったとしても石が余ってしまう(B-2A>0)からです。
後手が石を取ったら、先手は残った石を再び「隣合わないフィボナッチ数の和」で表し、その中の一番小さなフィボナッチ数の石を取ると、また後手は 残りの全てを取ることはできません。
すなわち、後手は常に勝てない状態で手を渡されていることになり、そのうち先手が全ての石を取ってゲーム終了となります。
なお、一般にすべての整数は「隣合わないフィボナッチ数の和」で表わせるらしいのです。
ここでは、1~20までのnに対する「隣合わないフィボナッチ数」の最小数fn(式1)がわかれば十分です。
f1=1
f2=2
f3=3
f4=1
f5=5
f6=1
f7=2
f8=8
f9=1
f10=2
f11=3
f12=1
f13=13
f14=1
f15=2
F16=3
f17=1
f18=5
f19=1
f20=2 (式1)(*2)
ここまで来て、先手必勝法の例外に気が付きました。
先手は、常に一番小さなフィボナッチ数を取ればよいのですが、次のルールにより取れない場合があります。
ルール1-先手の第1手目では、全部の石を取ってはいけない。
実は、先程の例(石の数が5個でゲームが始まった場合)がこれに相当します。「隣合わないフィボナッチ数の和」で表すと
5=0+0+0+5
なので、先手は5個すべて取るべきなのですが、ルール1により禁じられています。
つまり、先手必勝とは限らない場合があるということです。
もう1つ、先手必勝でない(かも知れない)点があります。
それは「もし、後手も同じ戦法を取った場合、後手必勝パターンで先手に手を渡せるのでは?」という点です。
深入りしたいところですが、理屈はここまでとします。
次回はプログラミングを行うことにします。
--------------------
(*1)以降、隣合わないかどうかが一目でわかるよう、使用しないフィボナッチ数も0として記載しています。
(*2)参考文献(翻訳本)「不思議な数列フィボナッチの秘密(日経BP社)」
■第8回 山崩しゲーム/本編(2017/01/04掲載,2022/04/07最終変更)
今回は山崩しゲームのプログラムを作成し動作させてみます。
ゲームの設計は、ほぼ第6回の説明の通りです。
具体的には、次のアルゴリズムとします。
ステップ1 ゲームの説明を表示する
ステップ2 乱数(範囲21~99)で石の初期値Nを決め、表示する
ステップ3 最初に人間に取る石の数Yを聞き、残りの石の数Nを計算・表示する、範囲外ならゲーム終了(ステップ10へ)
ステップ4 現在の石の数Nが21以上なら、コンピュータの取る石の数Iを10(ただし、上限2Y)とし、表示する
現在の石の数Nが20以下なら、コンピュータの取る石の数Iを最小フィボナッチ数(*1)(ただし、上限2Y)とし、表示する
ステップ5 残りの石の数Nを再計算・表示する、残り0なら人間の負け(ステップ8へ)
ステップ6 人間に取る石の数Yを聞き、ルール違反なら人間の負け(ステップ8へ)
ステップ7 残りの石の数Nを再計算・表示する、残り0ならコンピュータの負け(ステップ9へ)、そうでなければ継続(ステップ4へ)
ステップ8 人間の負けを表示、再ゲームへ(ステップ2へ)
ステップ9 人間の勝ちを表示、再ゲームへ(ステップ2へ)
ステップ10 プログラム終了
ステップ11 ディレイサブルーチン
また、プログラム中で使用している変数は次の通りです。
変数N(現在の石の数)
変数I(コンピュータの手)
変数Y(人間の手)
変数R(乱数計算用変数)
変数Z(キー入力待ちダミー変数)
変数J(コンピュータの手の計算補助)
変数S(サブルーチン戻り値退避)
以上で設計終了です。
では、この設計通りプログラミングしていきます。
【プログラム8】山崩しゲーム(#=1000で実行)
--- ゲームを開始するまでの準備(ステップ1~3) ---
(行番号1020、1170では、Enterキーを押すまで表示を止めています)
1000 (PROGRAM8)
1010 "YAMAKUZUSHI"
1020 Z=?
1100 (STEP1)
1110 R=0
1120 "AITENO TOTTA 2BAI";
1130 " MADE TORERU";
1140 Z=?
1150 "SAIGO WO TORU";
1160 " TO KACHI";
1170 Z=?
1200 (STEP2)
1210 N=@(R)
1220 N=N/3+21
1230 #=(N>99)*1220
1240 "STONE=";
1250 ?=N
1300 (STEP3)
1310 "YOU(1-";
1320 ?=N-1;
1330 ")?";
1340 Y=?
1350 R=R+Y
1360 #=(Y=0)+(Y=N)+(Y>N)*2100
1370 N=N-Y
1380 "STONE=";
1390 ?=N
--- ここから、勝敗が決まるまで繰り返す(ステップ4~7) ---
(行番号1420~1510は、本来1行で書けるはずなのですが、処理系の都合で10行に分けています)
1400 (STEP4)
1410 #=2200
1420 J=(N=1)+(N=4)+(N=6)+(N=9)
1430 J=(N=12)+(N=14)+(N=17)+J
1440 J=(N=19)+J
1450 J=(N=2)+(N=7)+(N=10)*2+J
1460 J=(N=15)+(N=20)*2+J
1470 J=(N=3)+(N=11)+(N=16)*3+J
1480 J=(N=5)*5+J
1490 J=(N=8)+(N=18)*8+J
1500 J=(N=13)*13+J
1510 J=(N>20)*10+J
1520 #=(2*Y<J)*1550
1530 I=J
1540 #=1560
1550 I=2*Y
1560 "I=";
1570 #=2200
1580 ?=I;
1600 (STEP5)
1610 #=2200
1620 ""
1630 N=N-I
1640 "STONE=";
1650 ?=N
1660 #=(N=0)*1900
1700 (STEP6)
1710 "YOU=";
1720 Y=?
1730 #=(Y=0)+(Y>N)*1900
1740 #=(2*I<Y)*1900
1800 (STEP7)
1810 N=N-Y
1820 "STONE=";
1830 ?=N
1840 #=(N=0)*2000
1850 #=1400
--- 以下は、終了処理(ステップ8~11) ---
1900 (STEP8)
1910 "**YOU LOSE**";
1920 Z=?
1930 #=1200
2000 (STEP9)
2010 "**YOU WIN**";
2020 Z=?
2030 #=1200
2100 (STEP10)
2110 "**END**"
2120 #=65535
2200 (STEP11)
2210 S=!
2220 L=0
2230 L=L+1
2240 #=(L<150)*2230
2250 #=S
このプログラムを動作させたところ、漠然とゲームを進めるだけでは、まずコンピュータに勝てません。
人間が先手なので圧倒的に有利なはずなのですが、コンピュータは石の数が20個以下になると正確に最適な石の数を取ってきます。
ちなみに、私は1回も勝たせてもらっていません。f(^_^; (*2)
次回はこのプログラムリストで使用したマイクロBASIC特有の表現(テクニック)について説明します。
--------------------
(*1)第7回の(式1)参照
(*2)2022年4月5日、このプログラムが初めて負けました。(しかも初戦で)
相手は数学科院卒、このような数学ゲームではたぶん最適スペックです。
理詰めで負けたので、何回対戦しても勝てないような気がします。
■第9回 山崩しゲーム/解説編(2017/02/04掲載,2017/02/05最終変更)
前回で、山崩しゲームのプログラミングは終了しました。
今回は、このプログラムで使用したマイクロBASIC特有の表現について説明します。(*1)
(1)条件分岐
マイクロBASICでは、GOTO文を、#=行番号と書きます。
これだけであれば、単に「GOTO」が代入式の表記(#=)に置き換わっただけなのですが、右辺に数式を書くことができます。
例えば
#=(A>10)*120
で、(A>10)の部分は論理式で、Aが10を超えるなら値1、Aが10以下なら値0となるので
Aが10を超えるなら、#=120
Aが10以下なら 、#=0
という意味になります。
マイクロBASICは、飛び先として行番号0を無視する仕様になっているので、Aが10を超えるときのみ行番号120へジャンプすることになります。
これは
IF A>10 THEN 120
と同じ動作をします。
この機能(飛び先として行番号0を無視する)のメリットは明確で、新たにIF文を実装する必要がないことです。本プログラムでは
1230 #=(N>99)*1220
などにこの構文を使っています。
(2)サブルーチン
マイクロBASICでは、GOTO文とGOSUB文は同じ表現(#=行番号)です。
GOSUB文をGOTO文と同じ表現にしたら、RETURN文のときに戻る行番号がスタックに積まれていないのでは?というあなたは正常です。
もちろんカラクリがあります。
実は、VTL言語処理プログラムは、#=行番号のとき変数!に現在の行番号+1の値を入れておきます。
このため、サブルーチンリターンのとき、#=!とするとサブルーチンをコールした行番号+1に戻ることができます。
欠点は、戻り先のスタックは1レベル(変数!)ですので、サブルーチン内で#=行番号を使えません。
もし使うと、変数!は上書きされてサブルーチンからリターンできなくなってしまいます。
回避策は、変数!が書き換えられる前に別の変数に退避しておくことです。本プログラムでは
1610 #=2200 ← GOSUB文に相当
…
2200 (STEP11)
2210 S=! ← サブルーチン内で#=を使うので、変数!を変数Sに退避
2220 L=0
2230 L=L+1
2240 #=(L<150)*2230 ← IF文に相当する#=を使う(変数!が壊れる)が、行番号2220で変数!は退避済み
2250 #=S ← RETUR文に相当
で、この構文を使っています。
マイクロBASICでは、GOTO文、IF~THEN文、GOSUB文、RUTURN文をすべて#=で済ませていることになります。(*1)
(3)AND、OR演算子
マイクロBASICでは、AND、ORがありません。例えば
IF (A=1)OR(A=3)OR(A=5) then 2000
を、マイクロBASICではORの代わりに+を使って
#=(A=1)+(A=3)+(A=5)*2000
と書きます。
もう、マイクロBASICに慣れたと思いますので説明不要かと思います。本プログラムでは
1360 #=(Y=0)+(Y=N)+(Y>N)*2100
などに、この構文を使っています。同様に、ANDは*が使えます。
さて、今回で山崩しゲームは終了とします。
次回は、変わったテーマを扱う予定です。(*2)
--------------------
(*1)#=行番号は、戻り先を記憶するスタックのサイズが1のGOSUB文で、#=!を使わなかった場合は「結果的に」GOTOと同じ動作をするというのが 本質的な解釈と思います。
(*2)参考文献
「エンサイクロペディア・アスキーVolume1、Altair680とマイクロBASIC(アスキー出版)」
■第10回 Brainfuck/準備編(2021/04/26掲載,2021/05/06最終変更)
以前、コラム「色々」の「たぶん世界で一番小さなプログラミング言語」の中で、VTL(マイクロBASIC)の話をしたときに「汎用的ではない小さなプログラミング言語(Brainfuckなど)があるらしいのですが、別世界ですのではここでは除外します」としていました。
今回は、この「別世界」の小さなプログラミング言語、BrainfuckのインタプリタをマイクロBASICで記述してみることにします。
言語仕様はプログラミングが難解なチューリングマシンの仲間か?って感じですが、この手の言語は「処理系は単純、プログラミングは茨の道」のはずです。
非力なマイクロBASICでも、処理系を作るのは意外と楽かもしれません。
構想としては、1つのマイクロBASICプログラムの中に、前半が「マイクロBASICで記述したBrainfuckインタプリタ」、後半が「Brainfuckで記述したプログラム」となるようにして実行することを考えています。
プログラムはざっくりとこんな感じです。(*3)
100 (ここから以降、マイクロBASICで記述したBrainfuckインタプリタ)
110
・・・
9999 [ここから以降、Brainfuckで記述したプログラム]
10000
10010
・・・
幸いなことに(?)マイクロBASICは文法チェックが緩いので、プログラムの後半がBrainfuckで記述したプログラムであっても、その行を実行しない限り気が付きません。f(^_^;
つまり、マイクロBASICのエディタがBrainfuckプログラム編集時にも使えます。
気になるのは、マイクロBASICの編集は、行ごとに行番号を付けてこれを目印編集(挿入、削除、上書)を行うことです。
Brainfuckプログラムにとっては、意味のない数字と空白がプログラムの各所に挿入されることになるのですが、Brainfuckは特定の記号以外を無視するので動作に影響無く、放置しておくことにしましょう。
次は、言語仕様です。
言語仕様については、ウィキペディアのBrainfuckの解説(https://en.wikipedia.org/wiki/Brainfuck)を参考にさせていただきました。(もちろん日本語に自動翻訳で)
ただ、今回は非力なマイクロBASICで実装するため、機能を落としています。
以下の言語仕様の説明では、最初からマイクロBASICで実装することを想定して、変数名などを具体的に表記しています。
【言語仕様】
(1)データメモリ
・データメモリとして、初期値が0の1次元配列@(0)~@(511)がある(*2)
・「命令が処理対象とするデータメモリ」の位置を示すデータポインタとして、初期値が0の変数Pがある
(2)プログラム
・命令は1文字の記号で表記し、命令を左から右に横に並べたものがプログラムである(*1)
・「これから実行すべき命令」の位置(のRAMアドレス)を示す命令ポインタとして、変数Qがある
(3)実行と停止
・プログラムは左端の命令から実行され、一部の例外(ジャンプ動作)を除いて、右に向かって順番に実行する
・命令以外の文字(英数字、空白、CRなど)が途中にあってもよいが、読み飛ばす
・右端の命令の次の命令を実行する直前で停止する
(4)命令
・命令と動作は表の通り。
| 命令 | 動作 (ジャンプ動作以外のときは、動作後Qに1を加算すること) |
| > | P=P+1 |
| < | P=P-1 |
| + | @(P)=@(P)+1 |
| - | @(P)=@(P)-1 |
| . | @(P)の値を、ASCIIコードと見なして端末装置に1文字出力 |
| , | 端末装置からの1文字入力を、ASCIIコードとして@(P)に書込 |
| [ | @(P)=0のときのみ、右方向の対応する"]"命令の次にジャンプ(Qを変更) |
| ] | @(P)≠0のときのみ、左方向の対応する"["命令の次にジャンプ(Qを変更) |
以上が、マイクロBASICで実現可能なBrainfuckの仕様です。
今一番のネックは、どうやって行番号9999以降のBrainfuckプログラムをマイクロBASICで読み出すか?です。
これについては、配列@のインデックスを操作することで、任意のRAMアドレスのデータを読み出すことを考えています。
--------------------
(*1)物理的にはRAMの特定アドレス(今回のマイクロBASICでは行番号9999以降)に記憶されたASCII表現の連続データです。
(*2)本来は「少なくとも30000個の「1バイトの要素」を持つ1次元配列」が必要です。
今回は処理系の都合で、これを「512個の「2バイトの要素」を持つ1次元配列」に変更しています。
(*3)インタプリタのサイズが予想より大きかったため、Brainfuckプログラムを「行番号999以降」から「行番号9999以降」に変更しました。
■第11回 Brainfuck/続準備編(2021/05/06掲載)
今回は、Brainfuckインタプリタを作成する上で、必要なサブルーチンを作成してゆきます。
これらのサブルーチンさえ作ってしまえば、Brainfuckインタプリタは9割出来上がったも同然です。)
(1)1バイト読出(サブルーチン)
最初に、指定したアドレス(0~4095番地)の1バイトデータをRAMから読み出すサブルーチンを作成します。
後で、このサブルーチンを使ってRAM上にあるBrainfuckプログラムを読み出すことになります。
実現方法は、配列@(ⅹ)のインデックスxを言語仕様の上限(ⅹ=895)を超えて「わざと配列以外のエリアをアクセス」します。
注意点は
・RAMアドレスは、4Kバイトの上限(10進数で4095番地)を超えると、次のアドレスが0,1,2,・・・番地であること
・配列@(x)は、要素1個あたりが2バイトであること
です。
では、RAMアドレスマップ見て見ましょう。
| アドレス (10進数) |
内容 |
| 0 ~263 |
作業領域、他 |
| 264 ~2049 |
マイクロBASICプログラム |
| 2048 ~3839 |
配列@(0)~@(895) |
| 3840 ~4095 |
マイコンの内部レジスタ |
マイクロBASICプログラムは264番地から格納されています。(*1)
もし、プログラム
10 A=12
20 ?=A
が入力されていれば、RAMアドレス264番地以降には、次の文字データが入っています。
| RAMアドレス | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 | 276 | 277 | 278 |
| データ | 1 | 0 | 空白 | A | = | 1 | 2 | CR | 2 | 0 | 空白 | ? | = | A | CR |
一方、配列の先頭@(0)は2048番地です。
この配列の先頭(2048番地)からRAM末尾(4095番地)までは、2047だけ番地が離れていて、さらに+1番地離れると(先頭に戻って)RAM先頭(0番地)に到達します。
ということは、プログラム先頭(264番地)までは、2047+1+264=2312だけ番地が離れていることになります。
したがって、プログラム先頭をアクセスするには、@(2312)としたいところですが「配列の要素は要素1個あたり2バイト」なので2で割った@(1156)がプログラム先頭となります。
| RAMアドレス | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 | 276 | 277 | 278 | 279 |
| 配列 | @(1156) | @(1157) | @(1158) | @(1159) | @(1160) | @(1161) | @(1162) | @(1163) | ||||||||
| データ | 1 | 0 | 空白 | A | = | 1 | 2 | CR | 2 | 0 | 空白 | ? | = | A | CR | (不定値) |
試しにダイレクトモードで
?=@(1156)
をキーインすると、2文字"10"をASCIIコードで表現されデータ3130Hの10進数表現
12592
が表示されます。
配列@(ⅹ)のインデックスxを操作することでRAMのデータが読み出せることが判ったところで、これをサブルーチン化します。
このサブルーチンは、RAMアドレスを変数Q(0~4095)から受け取ると、配列@(Q/2+1024)の2バイトを読み出します。
そして、偶数番地の場合は読み出した2バイトのうちの上位バイトを、奇数の場合は下位バイトを、変数Dに代入してリターンします。
【プログラム11 (1/7) 】1バイト読出(サブルーチン)
入力:変数Q(RAMアドレス、0~4095)、出力:変数D(読出データ、0~255)
1200 (READ 1BYTE)
1210 T=@(Q/2+1024)
1220 U=%
1230 D=T/256*(U=0)+(%*U)
1240 #=!
ここで、変数%は「直前の」割り算(/)実行結果の余り(除余)を意味します。
したがって行番号1230の実行直前で、アドレス(変数Q)が偶数ならU=0、奇数ならU=1になっています。
行番号1230の途中の%は、すでにT/256の割り算を実行しているので、読み出したデータの下位バイトに変化しています。
(2)プログラム先頭検索
前回説明した通り、Brainfuckプロラムは行番号9999以降に記述します。
これがRAMの何番地かを調べるプログラムを作成します。
動作は、マイクロBASICプログラムを1000番地から調べて、文字「9」(ASCIIコードで57)が4回連続して出現した時点で、その次のアドレスを変数Q(すなわち命令ポインタ)に入れて終了です。(*1)
これは、さっき作った「1バイト読出」を使います。
なお、このプログラムはメインプログラムの一部なのでサブルーチンではありません。
【プログラム11 (2/7) 】プログラム先頭検索
200 (SEARCH PRG TOP)
210 "SEARCH PRG..."
220 Q=1000
230 Q=Q+1
240 #=1200
250 #=(D=57)*270
260 #=230
270 Q=Q+1
280 #=1200
290 #=(D=57)*310
300 #=230
310 Q=Q+1
320 #=1200
330 #=(D=57)*350
340 #=230
350 Q=Q+1
360 #=1200
370 #=(D=57)*390
380 #=230
このプログラムを実行した直後、Brainfuckは命令ポインタ(変数Q)がプログラム左端の1番地手前(9999の最後の9)を示していることになります。
(3)命令( ] )検索(サブルーチン)
現在の命令ポインタ(変数Q)の次の命令から、Qが増加する方向に向かって対応する命令( ] )を探すサブルーチンを作成します。
このサブルーチンは、命令( [ )の処理の中で使用します。
次の(テキトーな)プログラムでは、左の赤字の命令( [ )の対応する命令( ] )は、右の赤字の命令( ] )です。
+[++[+++]++++]+++++
入れ子構造であっても正しく対応する命令( [ )を見つけるためには、出現した括弧をカウントする必要があります。
このためのカウンタ(変数C)は、検索中に命令( [ )が出現すればインクリメントし、検索中に命令( ] )が出現すればデクリメントします。
変数Cが0の時に見つけた命令( ] )が、対応する命令( ] )です。
ちなみに、 [ のASCIIコードは91、 ] のASCIIコードは93です。
【プログラム11 (3/7) 】命令( ] )検索(サブルーチン)
入力:変数Q(検索開始アドレス)、出力:変数Q(対応する命令( ] )のアドレス)
1100 (SEARCH ])
1110 S=!
1120 C=0
1130 Q=Q+1
1140 #=1200
1150 #=(D=93)*(C=0)*1180
1160 C=C+(D=91)-(D=93)
1170 #=1130
1180 #=S
(4)命令( [ )検索(サブルーチン)
もう、説明は不要かと思います。(3)と逆のサブルーチンです。
【プログラム11 (4/7) 】命令( [ )検索(サブルーチン)
入力:変数Q(検索開始アドレス)、出力:変数Q(対応する命令( [ )のアドレス)
1000 (SEARAH [)
1010 S=!
1020 C=0
1030 Q=Q-1
1040 #=1200
1050 #=(D=91)*(C=0)*1080
1060 C=C+(D=93)-(D=91)
1070 #=1030
1080 #=S
以上で準備は整いました。
次回は、Brainfuckの命令実行部分を作成しますが、単純な命令なので簡単です。
--------------------
(*1) プログラム先頭(264番地)から調べるのがわかりやすいのでが、プログラム前半部分はBrainfuckプロラムでないので(速度改善のため)途中から調べています。
■第12回 Brainfuck/本編(2021/05/06掲載,2021/05/09最終変更)
これまでで、Brainfuckインタプリタのかなりの部分が完成しました。
ここで、これから作るプログラムも含めて、行番号と機能の対応を表に整理してみました。
| 行番号 | 機能名 | 処理 |
| 100~ | スタート処理 | Brainfuckと表示、データメモリを初期化 |
| 200~ | プログラム先頭検索 | 行番号9999を検索、変数Qにアドレスをセット |
| 400~ | 命令読込・実行 | 変数Qの示す命令をフェッチ、実行を、終了(Q=&)まで繰り返す |
| 1000~ | 命令( [ )検索(サブルーチン) | 対応する命令( [ )を右方向へ検索、変数Qにアドレスをセット |
| 1100~ | 命令( ] )検索(サブルーチン) | 対応する命令( ] )を左方向へ検索、変数Qにアドレスをセット |
| 1200~ | 1バイト読出(サブルーチン) | 変数Qが示すRAMアドレスのデータを変数Dにセット |
| 9999~ | Brainfuckプログラム | サンプルプログラムとして入力文字の次のコードの文字を出力 |
今回は、Brainfuckインタプリタの残りの部分(スタート処理、命令読込・実行)を作成します。
(1)スタート処理
Brainfuckと表示、キーインを待ち、データメモリを初期化します。
特に難しい部分はありません。
【プログラム11 (5/7) 】スタート
100 (PROGRAM11)
110 "Brainfuck"
120 "INIT DATA..."
130 P=0
140 @(P)=0
150 P=P+1
160 #=(P<512)*140
170 P=0
(2)命令読込・実行
インタプリタの核心部分です。
このプログラムは「プログラム先頭検索」プログラムの直後に実行するので、Qはプログラム左端ー1の位置から開始します。
手順は
・変数Q(命令ポインタ)を+1
・プログラム末になったら「スタート処理」の先頭に戻る(*2)
・変数Qの示す命令を読み出す
・命令を実行
・元に戻る
です。
なお、命令( . )と命令( , )では、「1文字入力(>=59)」と「1文字出力((>=62)」のシステムコールを使用しています。(引数、戻り値は変数%)
【プログラム11 (6/7) 】命令読込・実行
400 (FETCH & EXEC)
410 "RUN..."
420 Q=Q+1
430 #=(Q=&)*110
440 #=1200
450 #=(D=62)*550
460 #=(D=60)*600
470 #=(D=43)*650
480 #=(D=45)*700
490 #=(D=46)*750
500 #=(D=44)*800
510 #=(D=91)*850
520 #=(D=93)*900
530 #=420
550 (>)
560 P=P+1
570 #=420
600 (<)
610 P=P-1
620 #=420
650 (+)
660 @(P)=@(P)+1
670 #=420
700 (-)
710 @(P)=@(P)-1
720 #=420
750 (.)
760 %=@(P)
770 >=59
780 #=420
800 (,)
810 >=62
820 @(P)=%
830 #=420
850 ([)
860 #=@(P)=0*1100
870 #=420
900 (])
910 #=@(P)>0*1000
920 #=420
参考までに、本プログラム中で使用する文字データのASCIIコード (10進数表現)を表に纏めておきます。
| 命令 | ASCIIコード |
| > | 62 |
| < | 60 |
| + | 43 |
| - | 45 |
| . | 46 |
| , | 44 |
| [ | 91 |
| ] | 93 |
以上で、Brainfuckインタプリタは完成です。
プログラム11(1/7)~(6/7)を行番号の小さい順に並べた全体がインタプリタとなります。
(3)Brainfuckプログラム
このインタプリタが実行するプログラムを行番号999以降に記述します。
ここでは、サンプルプログラムとして「入力文字の次のコードの文字を出力する」プログラムを記述しておきます。
Enterキー入力でプログラムを終了します。
【プログラム11 (7/7) 】Brainfuckプログラム
9999 [Brainfuck Program]
10000 +[,+.]
HALと1文字ずつゆっくり入力してIBMと表示されれば、とりあえず正しく動いています。(*1)
超遅いプログラムなのでショックかも知れません。
なお、プログラム11(1/7)~(7/7)は、このページの先頭からダウンロードできます。
次回は、いくつかのサンプルプログラムで、このインタプリタの動作検証を行う予定です。
動作検証前のコードですので、今後改良・修正するかも知れないことをご了承ください。
では、また。
--------------------
(*1) HALの説明は不要ですよね。
(*2)第13回でプログラムを改造したときに「プログラム末になったら、マイクロBASICのダイレクトモードに戻る」に仕様を変更しました。
■第13回 Brainfuck/改造編(2021/05/09掲載)
今回は、いくつかのサンプルプログラムを動かしてBrainfuckインタプリタの動作検証を行う予定でした。
でも、Brainfuckインタプリタが余りにも遅く、動作検証プログラムがまともな速度で動きません。
そこで方針を変更し、先にBrainfuckインタプリタに対し、処理速度の足を引っ張っている箇所の改造を行うことにしました。
具体的には、次の3項目の改造を行いました。
(1)頻繁にジャンプするプログラム(の飛び先)をプログラムの先頭に移す
「#=行番号」の書式でジャンプすると、マイクロBASICインタプリタはジャンプ先の行番号を見つけるために、プログラムを先頭から順に読んでゆきます。
したがって、頻繁にジャンプする飛び先は、プログラムの先頭近くに配置した方が(言い換えると、行番号が小さい方が)早く見つかるので、処理速度が上がります。
そこで、機能ごとに割り当てている行番号を表の通り変更し、プログラムの行番号を書き換えました。
| 機能名 | 行番号 (変更前) |
行番号 (変更後) |
| スタート処理 | 100~ | 10~,2100~ |
| プログラム先頭検索 | 200~ | 2200~ |
| 命令読込・実行 | 400~ | 400~ |
| 命令( [ )検索(サブルーチン) | 1000~ | 200~ |
| 命令( ] )検索(サブルーチン) | 1100~ | 300~ |
| 1バイト読出(サブルーチン) | 1200~ | 100~ |
| Brainfuckプログラム | 9999~ | 9999~ |
(2)小さい数で割り算を行わないようする
マイクロBASICインタプリタは、割り算(/)処理を引き算の繰り返しで実現しています。(*1)
この方法は処理は簡単ですが、大きい数を小さい数で割る場合に繰り返し回数が多くなり、処理速度が低下します。
例えば65535/2の計算だと、1回の除算に3万回以上のループを行っていることになります。
実は、この2で割る演算(Q/2)が行番号1210にありました。(この時のQはたぶん数千程度)
1130 Q=Q+1
1140 #=1200
・・・
1200 (READ 1BYTE)
1210 T=@(Q/2+1024)
1220 U=%
1230 D=T/256*(U=0)+(%*U)
1240 #=!
「2での割り算」をマイクロBASICにさせないために「命令ポインタQの代わりに、最初からQの半分の値であるRと、偶数/奇数で値0/1をとる変数Kを使う」ことにしました。
つまり、Q=R×2+Kの関係です。
こうすれば、さっきの1210行は「T=@(R+1024)」と書けるため、/2の除算をしなくて済みます。
では、Qを使わなくなったら、行番号1130のQ=Q+1はどうやって書けばよいかというと「K=(K=0)」「R=R+(K=0)」です。
Rが2回に1回しかインクリメントされないのが判ると思います。
ということで、先程のプログラム全体は次の通りとなります。(行番号を(1)で書き換えた後なので、行番号が異なっています)
330 K=(K=0)
335 R=R+(K=0)
340 #=100
・・・
100 (READ 1BYTE)
110 T=@(R+1024)
120 D=T/256*(K=0)+(%*K)
130 #=!
コール側は数か所あるので、すべて同様に書き換えます。(Q=Q-1も同様)
(3)プログラム実行開始時にBrainfuckプログラムの先頭を見つけるまでの時間を短縮する
これは、従来からQ=1000から探すようにしていましたが、実質Q=1600前後がBrainfuckプログラムの先頭であるため
2220 R=750
2225 K=0
から検索するようにしました。
Qに換算すると、Q=1500から探していることになります。
以上で処理速度の足を引っ張っている箇所の改造が終わりました。
実際に走らせてみたところ、確かに応答速度は早くなりましたが、サクサクと動いている感じではありません。(*2)
改造後のプログラム13は、このページの先頭からダウンロードできます。
次回は、いくつかのサンプルプログラムで、このインタプリタの動作検証です。
--------------------
(*1)普通は、CPUの除算命令を使うか、除算命令が無い場合は筆算で割り算を行うようなアルゴリズム(引き戻し法)で計算する、のが一般的かと思います。
(*2)「命令読込・実行」をアセンブラで書きたいところですが「マイクロBASICによる数値計算とゲーム」の主旨とはちょっと離れるのでここではしません。
■第14回 Brainfuck/実行編(2021/11/06掲載,2021/11/07最終変更)
8ビットマイコンで動作するマイクロBASICで、Brainfuckインタプリタを記述し、その上でBrainfuckプログラムを走らせるというテーマも今回が最後です。
今回は、簡単なBrainfuckプログラムを実行してみることにします。
具体的には、プログラム13をマイクロBASICにロードした後、行番号10000以降をプログラム(14-1または14-2)に置き換えて実行(#=1)させます。
【プログラム14ー1】3文字入力後、3回表示
(9999行まではプログラム13と同じ)
10000 +[++>,>,>,<<<
10010 [>.>.>.<<<-]+]
今回、初めて「>」「<」「-」を使っています。
また、括弧の「入れ子」もは初めてで、これらの動作チェックを兼ねています。
動作は
(1)1番目のセルに3を代入
(2)3文字入力し、2~4番目のセルに代入
(3)2~4番目のセルの文字を表示
(4)1番目のセルから1を引きその結果が0でなければ(3)に戻る
(5)(1)に戻る
です。
実行結果を下図に示します。
(「HAL」と3文字キー入力すると、「HALHALHAL」と表示します。123、abcも同様です。)
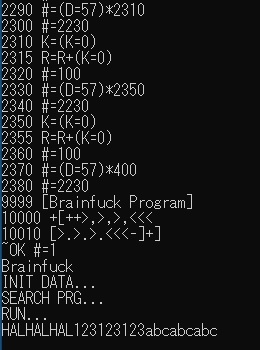
では、次のプログラムです。
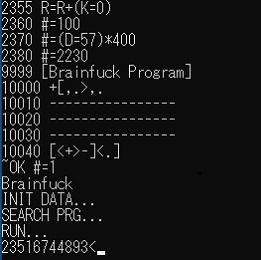
【プログラム14ー2】1桁の加算
(9999行まではプログラム13と同じ)
10000 +[,.>,.
10010 ----------------
10020 ----------------
10030 ----------------
10040 [<+>-]<.]
数字(1~8の範囲)を2個キー入力すると、その加算結果を表示します。(ただし、結果は2~9の範囲)
動作説明は省略、自分で考えてください。(ヒントは、文字コードに直接加算しています)
実行結果を下図に示します。
(2+3=5、1+6=7、4+4=8を計算し、最後は9+3=12でわざとオーバーフローさせています)(*1)
今回で、Brainfuckはおしまいです。
頑張った割には、あまり見栄えのする成果がなかったのが残念ですが、久しぶりに異質のプログラミング言語を体験できました。(ラダー図以来かな…)
次回、何をするかは決まっていませんが、別のテーマとなる予定です。
--------------------
(*1)ASCIIコード表を見れば、9+3の結果が「12」ではなく「<」になったがが判ります。
■第15回 素数の計算(2022/03/27掲載,2022/03/29最終変更)
今回は、1000までの素数(Prime)を計算してみます。
素数の定義ですが、ここでは「2以上の自然数Nのうち、これを2~Nー1の自然数で割ったとき、必ず割り切れずに余りが発生する数」とします。
ただし、N=2だけは無条件で素数とします。
回りくどい言い方ですが、これから書くプログラムとの整合性を意識しています。
定義としては間違っていないはずです。
さて、プログラムは素数の候補を変数Pとし、これを変数X(値は2からP-1まで変化)で割り切れるか調べています。
マイクロBASICに慣れた皆さんには普通に読めるかと思います。
念のため、1箇所だけ説明しておくと
1090 T=P/X
1100 #=%=0*1050
で、1090行では「素数の候補PがXで割り切れるか調べるためにダミーの変数を使って「T=P/X」を計算しています。
これを実行すると、(マイクロBASICの仕様により)直前に実行した割り算の余りが変数%に格納されるので、変数%が0かどうかで、割り切れたかどうかの判定ができます。
1100行はこの条件分岐で「#=(%=0)*1050」と書いた方が解りやすかもしれません。
【プログラム15】素数の計算(#=1000で実行)
1000 (PROGRAM15)
1010 "PRIME"
1020 P=2
1030 ?=P;
1040 " ";
1050 P=P+1
1060 X=1
1070 X=X+1
1080 #=X=P*1030
1090 T=P/X
1100 #=%=0*1050
1110 #=1070
実行すると、画面上に2から順に素数を表示してゆきます。
PRIME
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997 1009 OK
実行してから16分ちょっとで素数が1000を超えたので、Escキーを押してマイクロBASICの実行を中断しました。
3桁の最大の素数は997でした。
当然のことですが、数が大きくなるほど計算時間がかかります。
この後、再実行させたところ、一晩で6427まで計算しました。(*1)
--------------------
(*1)5000までの結果は次の通りです。
PRIME
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997 1009 1013 1019 1021 1031 1033 1039 1049 1051 1061 1063 1069 1087 1091 1093 1097 1103 1109 1117 1123 1129 1151 1153 1163 1171 1181 1187 1193 1201 1213 1217 1223 1229 1231 1237 1249 1259 1277 1279 1283 1289 1291 1297 1301 1303 1307 1319 1321 1327 1361 1367 1373 1381 1399 1409 1423 1427 1429 1433 1439 1447 1451 1453 1459 1471 1481 1483 1487 1489 1493 1499 1511 1523 1531 1543 1549 1553 1559 1567 1571 1579 1583 1597 1601 1607 1609 1613 1619 1621 1627 1637 1657 1663 1667 1669 1693 1697 1699 1709 1721 1723 1733 1741 1747 1753 1759 1777 1783 1787 1789 1801 1811 1823 1831 1847 1861 1867 1871 1873 1877 1879 1889 1901 1907 1913 1931 1933 1949 1951 1973 1979 1987 1993 1997 1999 2003 2011 2017 2027 2029 2039 2053 2063 2069 2081 2083 2087 2089 2099 2111 2113 2129 2131 2137 2141 2143 2153 2161 2179 2203 2207 2213 2221 2237 2239 2243 2251 2267 2269 2273 2281 2287 2293 2297 2309 2311 2333 2339 2341 2347 2351 2357 2371 2377 2381 2383 2389 2393 2399 2411 2417 2423 2437 2441 2447 2459 2467 2473 2477 2503 2521 2531 2539 2543 2549 2551 2557 2579 2591 2593 2609 2617 2621 2633 2647 2657 2659 2663 2671 2677 2683 2687 2689 2693 2699 2707 2711 2713 2719 2729 2731 2741 2749 2753 2767 2777 2789 2791 2797 2801 2803 2819 2833 2837 2843 2851 2857 2861 2879 2887 2897 2903 2909 2917 2927 2939 2953 2957 2963 2969 2971 2999 3001 3011 3019 3023 3037 3041 3049 3061 3067 3079 3083 3089 3109 3119 3121 3137 3163 3167 3169 3181 3187 3191 3203 3209 3217 3221 3229 3251 3253 3257 3259 3271 3299 3301 3307 3313 3319 3323 3329 3331 3343 3347 3359 3361 3371 3373 3389 3391 3407 3413 3433 3449 3457 3461 3463 3467 3469 3491 3499 3511 3517 3527 3529 3533 3539 3541 3547 3557 3559 3571 3581 3583 3593 3607 3613 3617 3623 3631 3637 3643 3659 3671 3673 3677 3691 3697 3701 3709 3719 3727 3733 3739 3761 3767 3769 3779 3793 3797 3803 3821 3823 3833 3847 3851 3853 3863 3877 3881 3889 3907 3911 3917 3919 3923 3929 3931 3943 3947 3967 3989 4001 4003 4007 4013 4019 4021 4027 4049 4051 4057 4073 4079 4091 4093 4099 4111 4127 4129 4133 4139 4153 4157 4159 4177 4201 4211 4217 4219 4229 4231 4241 4243 4253 4259 4261 4271 4273 4283 4289 4297 4327 4337 4339 4349 4357 4363 4373 4391 4397 4409 4421 4423 4441 4447 4451 4457 4463 4481 4483 4493 4507 4513 4517 4519 4523 4547 4549 4561 4567 4583 4591 4597 4603 4621 4637 4639 4643 4649 4651 4657 4663 4673 4679 4691 4703 4721 4723 4729 4733 4751 4759 4783 4787 4789 4793 4799 4801 4813 4817 4831 4861 4871 4877 4889 4903 4909 4919 4931 4933 4937 4943 4951 4957 4967 4969 4973 4987 4993 4999
■第16回 自然対数の底eの計算(2022/03/27掲載)
e(自然対数の底、別名「ネイピア数」、2.7182818284…)は、本来の定義とは別に、次の無限級数(マクローリン級数)で表現できることが知られています。
e=(1/0!)+(1/1!)+(1/2!)+(1/3!)+…
この右辺がなぜeになるのか?チンプンカンプンなのですが、そこはスルーして、今回はこの式を前提に整数しか扱えないマイクロBASICで計算してみます。
式を見ると、1を2!や3!で割っている項がありますが、何も工夫せずに整数演算すると結果は0になってしまいます。
そこで、円周率(π)の計算をしたときと同じく、両辺に定数を掛けて整数演算だけで計算できるように式を変形します。
ここでは、両辺に10000掛けます。
10000e=(10000/0!)+(10000/1!)+(10000/2!)+(10000/3!)+… (式1)
この式の右辺を見ると、今度は10000を2!や3!で割っていますので、各項の値は0ではなくそれらしい数になっています。
10000e=(10000/1)+(10000/1)+(10000/2)+(10000/6)+…
=10000+10000+5000+1666+… (式1)
最初の4項の和だけで26666(4桁ずらして読むと2.6666)となり、かなり2.7828に近づいていて期待できそうです。
ただ、この式にも1つ問題があります。
各項の分子が(階乗なので)急速に大きくなり、あっという間にマイクロBASICの扱える数値の上限65535を超えてしまいます。
ちゃんと計算(*1)したところ、8!=40320なので、ここで計算を打ち切っています。
プログラムは、N=1~8までのF=N!を計算し、それぞれの10000/Fの値の合計Eを求めてます。(*2)
【プログラム16】自然対数の底eの計算(マクローリン級数)(#=2000で実行)
2000 (PROGRAM16)
2010 "NAPIER"
2020 N=0
2030 F=1
2040 E=10000
2050 ?=N;
2060 " ";
2070 ?=F;
2080 " ";
2090 ?=E
2100 N=N+1
2110 F=F*N
2120 E=E+(10000/F)
2130 #=(N<9)*2050
2140 #=50000
実行すると、一瞬で計算が終了しました。
NAPIER
0 1 10000
1 1 20000
2 2 25000
3 6 26666
4 24 27082
5 120 27165
6 720 27178
7 5040 27179
8 40320 27179
OK
右下の数値を4桁ずらして読むと2.7179となり、これが自然対数の底eの計算結果です。
真値(2.7182818284…)とは、3桁(2.71まで)一致しました。
今回は、ちょこっとしたテーマでした。
--------------------
(*1)ここはちゃっかり、パソコンで計算しました。f(^_^;
(*2)(式1)の右辺の第1項に0の階乗(0!)が現れますが、数学上、0の階乗は値1と定義されています。
でも、1×2×3×…という計算方法では0!を計算できませんので、プログラム16では、(式1)の右辺の第1項を最初から1(プログラム上は、E=10000)としています。
■第17回 スライドパズル(2025/03/30掲載,2025/04/01最終変更)
今回は、3×3のスライドパズルをプログラミングしてみます。
スライドパズルと言われてもピンとこない人も、たぶん一度はトライしたことのある簡単なパズルです。
3×3なので、1から8までの数字が各1個と空白が1個を、3×3のマス目にランダムに配置された状態からスタートします。
例えば初期状態が
241
83
765
とすると、空白のマス目に動かせる数字は赤字の2と8と7のみです。(4と6は斜め移動なので物理的に無理)
ここで、数字8を空白に移動させると
241
8 3
765
となり、今度は空白のマス目に動かせる数字は赤字の4と8と3と6になります。
これ繰り返して最終的に次のように1から8が昇順に並べはパズルは完成です。
123
456
78
これを、マイクロBASICでプログラミングしてみようというのが今回のテーマです。
では、プログラムの説明に移ります。
まず、扱うパズルは3×3の2次元座標なので2次元配列に現在置かれている数字を記憶させるのが素直なのですが、残念ながらマイクロBASICは1次元配列しか扱えません。
そこで、3×3のマス目と座標は次の通りとし
座標0 座標1 座標2
座標3 座標4 座標5
座標6 座標7 座標8
この座標0~座標8に置かれた数字を記憶する配列を次のように決めます。
@(0) @(1) @(2)
@(3) @(4) @(5)
@(6) @(7) @(8)
@(0)~@(8)は0~8のいずれかの値で、0のときは空白を意味します。
次に、今回のプログラムで使用する変数の意味は、次の通りとします。
変数C (数字を移動した操作回数)
変数X(1~8のどの数字を移動するかキー入力した値)
変数I(判定&移動サブルーチンで使う、空白のマス目の「座標」0~8)
変数J(判定&移動サブルーチンで使う、空白のマス目の「座標」が指定されたとき、その周囲で空白の位置に移動可能な数字の「座標」0~8)
変数R (判定&移動サブルーチンの戻り行番号(!)を保存)
変数N、変数M (作業変数)
アルゴリズムは次の通りとしました。
ステップ1(行番号15~) パズルの初期状態を決定する
ステップ2(行番号100~) タイトルを表示後、キー入力(0~999)を要求し、その値で適当に数字を入れ替える(これでパズルの初期状態をランダムに見せる)
ステップ3(行番号200~) 何回目の操作かを表示後、現在のマス目(3×3)のj状態を画面表示する
ステップ4(行番号300~) どの数字を空白の位置に動かすかをキー入力し、1~8なら次のステップへ(ステップ5へ)、99ならパズルを再スタート(ステップ2へ)、それ以外ならキー入力やり直しとする
ステップ5(行番号350~) 座標0が空白で、周囲の数字が空白に動かせるなら動かしてステップ3へ、動かせなければ次のステップへ
ステップ6(行番号400~) 座標1が空白で、周囲の数字が空白に動かせるなら動かしてステップ3へ、動かせなければ次のステップへ
ステップ7(行番号450~) 座標2が空白で、周囲の数字が空白に動かせるなら動かしてステップ3へ、動かせなければ次のステップへ
…
ステップ12(行番号800~) 座標8が空白で、周囲の数字が空白に動かせるなら動かしてステップ3へ、動かせなければ「動かせんません」と表示してステップ4へ
なお、行番号850~はステップ5~12で使用する「判定&移動」サブルーチン(*1)です。
プログラムリスト(list_su5.txt)は、本ページの先頭付近の「記事中のプログラム・資料」からダウンロードできます。
ターミナルソフト(ZTERM!)を使用すると、ダウンロードしたプログラムをマイコンボードにロード(*2)することができます。
実行結果を下図に示します。
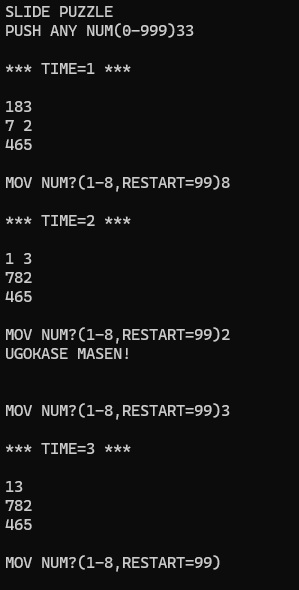
スライドパズルはどうやっても、完成しないパターンがあるそうです。
このプログラムは、完成しないパターンを除外するといった処理を行っていません。
途中で完成しないパターンみたいだなだと思ったら「MOV NUM?」と聞かれたとき「99」を押して最初からやり直すしかありません。
--------------------
(*1)このサブルーチンでは、数字を移動できた場合に限りメインルーチンに「リターン」ではなく、サブルーチンコールした行番号と全く関係のない行番号へ「ジャンプ」で戻るという荒業を行っています。
サブルーチンコールにスタックを使わないマイクロBASICだから可能なプログラムです。
もし他の言語に置き換える場合はこの部分は書き換えが必要です。
(*2)この「スライドパズル」のプログラム開発中に、ターミナルソフトZTERM!の「PC-→BOARD」機能を使ってプログラムをマイコンボードにロードすると、プログラム末近くの行番号が文字化けする、という不具合を発見しました。
原因はプログラムが長いとマイコンボード側のプログラムロード処理が間に合わないためと推測しています。
今回の開発では、プログラムの行番号をできるだけ小さい番号に書き換えることで、この不具合を回避しました。(list_su5.txtのみ、他のプログラムに比べて行番号が小さくなっているのはこのためです)
現在、この不具合の回避方法はこの方法しかありませんが、ご了承願います。